Note
Go to the end to download the full example code
Estimation des paramètres d’un mélange de modèles SIRD¶
Le virus mute et certains variantes sont plus contagieuses.
Dans ce modèle, on simule une population au sein de laquelle
circulent deux virus avec le modèle suivant :
CovidSIRDMixture.
L’idée est ensuite d’estimer un module plus simple
sur cette population pour comprendre comment le paramètre
\(\beta\) de ce modèle simple évoluerait.
Simulation des données¶
import warnings
from pprint import pprint
import numpy
import matplotlib.pyplot as plt
import pandas
from aftercovid.models import EpidemicRegressor, CovidSIRDMixture
model = CovidSIRDMixture()
model
Mise à jour des coefficients.
model['beta1'] = 0.15
model['beta2'] = 0.25
model["mu"] = 0.06
model["nu"] = 0.04
pprint(model.P)
[('beta1', 0.15, 'taux de transmission dans la population'),
('beta2', 0.25, 'second taux de transmission dans la population'),
('mu', 0.06, '1/. : durée moyenne jusque la guérison'),
('nu', 0.04, "1/. : durée moyenne jusqu'au décès")]
Point de départ
pprint(model.Q)
[('S', 9990.0, 'personnes non contaminées'),
('I1',
8.0,
'nombre de personnes malades ou contaminantes pour le premier variant'),
('I2',
2.0,
'nombre de personnes malades ou contaminantes pour le second variant'),
('R', 0.0, 'personnes guéries (recovered)'),
('D', 0.0, 'personnes décédées')]
On part d’un point de départ un peu plus conséquent car l’estimation n’est pas très fiable au départ de l’épidémie comme le montre l’exemple Estimation des paramètres d’un modèle SIRD.
model.update(S=9100, I1=80, I2=20)
pprint(model.Q)
[('S', 9100.0, 'personnes non contaminées'),
('I1',
80.0,
'nombre de personnes malades ou contaminantes pour le premier variant'),
('I2',
20.0,
'nombre de personnes malades ou contaminantes pour le second variant'),
('R', 0.0, 'personnes guéries (recovered)'),
('D', 0.0, 'personnes décédées')]
Simulation
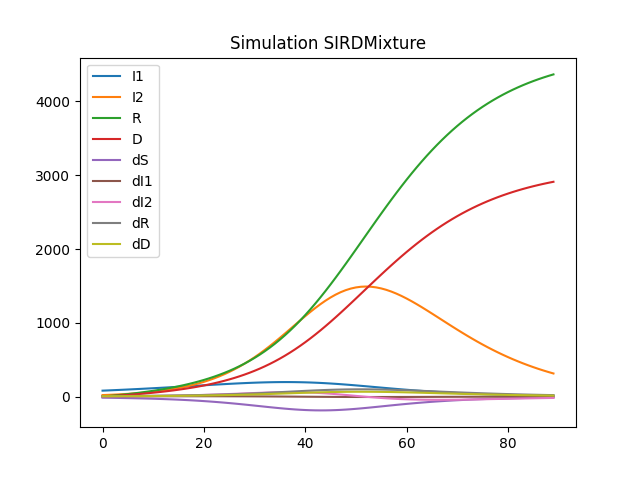
Visualisation
df.drop('S', axis=1).plot(title="Simulation SIRDMixture")
Estimation¶
Le module implémente la class EpidemicRegressor qui réplique
l’API de scikit-learn. Il faut additionner
I1 et I2.
X2 = numpy.empty((X.shape[0], 4), dtype=X.dtype)
X2[:, 0] = X[:, 0]
X2[:, 1] = X[:, 1] + X[:, 2]
X2[:, 2] = X[:, 3]
X2[:, 3] = X[:, 4]
y2 = numpy.empty((y.shape[0], 4), dtype=X.dtype)
y2[:, 0] = y[:, 0]
y2[:, 1] = y[:, 1] + y[:, 2]
y2[:, 2] = y[:, 3]
y2[:, 3] = y[:, 4]
X, y = X2, y2
m = EpidemicRegressor('SIRD', verbose=True, learning_rate_init=1e-3,
max_iter=15, early_th=1)
m.fit(X, y)
pprint(m.model_.P)
0/15: loss: 3.181e+06 lr=1.13e-09
1/15: loss: 1.025e+06 lr=1.13e-09
2/15: loss: 2.874e+05 lr=1.13e-09
3/15: loss: 7.064e+04 lr=1.13e-09
4/15: loss: 2.012e+04 lr=1.13e-09
5/15: loss: 7880 lr=1.13e-09
6/15: loss: 5070 lr=1.13e-09
7/15: loss: 4449 lr=1.13e-09
8/15: loss: 4277 lr=1.13e-09
9/15: loss: 4229 lr=1.13e-09
10/15: loss: 4214 lr=1.13e-09
11/15: loss: 4209 lr=1.13e-09
12/15: loss: 4222 lr=1.13e-09
13/15: loss: 4212 lr=1.13e-09
14/15: loss: 4208 lr=1.13e-09
15/15: loss: 4229 lr=1.13e-09
[('beta', 0.21389042254426982, 'taux de transmission dans la population'),
('mu', 0.0593583064407937, '1/. : durée moyenne jusque la guérison'),
('nu', 0.0393583068370424, "1/. : durée moyenne jusqu'au décès")]
La réaction de la population n’est pas constante tout au long de l’épidémie. Il est possible qu’elle change de comportement tout au long de la propagation. On estime alors les coefficients du modèle sur une fenêtre glissante.
def find_best_model(Xt, yt, lrs, th):
best_est, best_loss = None, None
for lr in lrs:
with warnings.catch_warnings():
warnings.simplefilter("ignore", RuntimeWarning)
m = EpidemicRegressor(
'SIRDc',
learning_rate_init=lr,
max_iter=500,
early_th=1)
m.fit(Xt, yt)
loss = m.score(Xt, yt)
if numpy.isnan(loss):
continue
if best_est is None or best_loss > loss:
best_est = m
best_loss = loss
if best_loss < th:
return best_est, best_loss
return best_est, best_loss
On estime les coefficients du modèle tous les 5 jours sur les 10 derniers jours.
coefs = []
for k in range(0, X.shape[0] - 9):
end = min(k + 10, X.shape[0])
Xt, yt = X[k:end], y[k:end]
m, loss = find_best_model(Xt, yt, [1e-2, 1e-3], 10)
loss = m.score(Xt, yt)
print(f"k={k} iter={m.iter_} loss={loss:1.3f} coef={m.model_._val_p}")
obs = dict(k=k, loss=loss, it=m.iter_, R0=m.model_.R0())
obs.update({k: v for k, v in zip(m.model_.param_names, m.model_._val_p)})
coefs.append(obs)
k=0 iter=113 loss=0.890 coef=[ 0.16800033 0.06174018 0.04021276 -0.01798747 0. 0.01481924]
k=1 iter=76 loss=0.897 coef=[ 1.63566671e-01 5.70162350e-02 4.06674426e-02 -2.26503170e-06
5.49368634e-03 0.00000000e+00]
k=2 iter=101 loss=1.486 coef=[ 0.17180541 0.06138432 0.03815742 -0.04328613 0. 0.03362906]
k=3 iter=72 loss=1.197 coef=[ 0.17160838 0.06049221 0.04031133 -0.01581161 0. 0.00319452]
k=4 iter=71 loss=1.444 coef=[ 0.17328034 0.06033304 0.04000865 -0.02274334 0. 0.00562844]
k=5 iter=64 loss=1.906 coef=[ 0.17621065 0.05909734 0.03903453 -0.03768507 0. 0.00345754]
k=6 iter=65 loss=2.598 coef=[ 0.17805187 0.05844313 0.03804139 -0.0558203 0. 0.00775403]
k=7 iter=62 loss=2.668 coef=[ 0.1797094 0.06235479 0.0379265 -0.02347976 0. 0.06064533]
k=8 iter=48 loss=3.260 coef=[ 0.18167883 0.05829371 0.03805053 -0.05047896 0. 0.00520038]
k=9 iter=45 loss=2.717 coef=[ 0.18156135 0.0599281 0.03939319 -0.01604502 0. 0.00934677]
k=10 iter=41 loss=5.033 coef=[ 0.18467887 0.0586739 0.03772353 -0.06065985 0. 0.01632678]
k=11 iter=35 loss=3.417 coef=[ 1.84547448e-01 5.98286153e-02 3.99691250e-02 -1.10283608e-03
1.29925010e-05 1.04560286e-03]
k=12 iter=34 loss=4.382 coef=[ 1.87179691e-01 5.87582600e-02 3.83802254e-02 -3.06245684e-02
2.03826248e-05 7.04713377e-03]
k=13 iter=24 loss=7.848 coef=[ 0.19189258 0.05735833 0.03696538 -0.06450875 0. 0.00735225]
k=14 iter=22 loss=5.170 coef=[ 0.19004676 0.05985992 0.0389666 -0.0216856 0. 0.01425076]
k=15 iter=25 loss=8.199 coef=[ 0.19349448 0.05845787 0.03790081 -0.05297498 0. 0.01004378]
k=16 iter=21 loss=6.039 coef=[ 1.93581057e-01 6.15311929e-02 3.91961772e-02 -6.18545644e-03
4.18219895e-05 4.03800338e-02]
k=17 iter=15 loss=6.631 coef=[ 1.95104311e-01 6.02214717e-02 3.91460522e-02 -2.99157511e-03
7.24107759e-05 1.83051089e-02]
k=18 iter=16 loss=6.597 coef=[ 1.95858765e-01 5.99331658e-02 4.00137667e-02 -2.80838526e-03
1.51248450e-04 1.98532975e-04]
k=19 iter=18 loss=8.646 coef=[ 0.19701958 0.05886694 0.03875698 -0.02434081 0.00039036 0.00218985]
k=20 iter=13 loss=7.749 coef=[ 0.198812 0.06089266 0.03973979 -0.00067957 0.00038875 0.01728366]
k=21 iter=18 loss=10.134 coef=[ 0.20226278 0.05877008 0.03853194 -0.02837214 0.00127666 0.00446293]
k=22 iter=90 loss=12.868 coef=[ 0.2041831 0.05877042 0.0385441 -0.04037408 0. 0.00428015]
k=23 iter=79 loss=9.929 coef=[ 2.04535742e-01 5.95187719e-02 3.91879483e-02 -1.95186954e-02
1.66647809e-07 5.49473756e-03]
k=24 iter=17 loss=9.300 coef=[ 0.204609 0.05951479 0.03928662 -0.00871614 0.00267565 0.00475083]
k=25 iter=15 loss=12.680 coef=[ 0.20655414 0.05969885 0.03930789 -0.02362833 0.0014867 0.00750289]
k=26 iter=64 loss=11.582 coef=[ 0.20835778 0.05975053 0.03900209 -0.02023028 0. 0.0127213 ]
k=27 iter=62 loss=13.645 coef=[ 0.20870402 0.05909773 0.03836741 -0.0260821 0. 0.01252683]
k=28 iter=17 loss=12.838 coef=[ 0.21087256 0.05962211 0.03873243 -0.01655748 0.0007514 0.01554695]
k=29 iter=24 loss=12.507 coef=[ 0.21071283 0.06086267 0.03959953 -0.01117438 0.0007223 0.02194175]
k=30 iter=20 loss=12.460 coef=[ 2.11568931e-01 6.14474562e-02 3.86821733e-02 -3.61796591e-03
8.99198411e-05 4.80763086e-02]
k=31 iter=27 loss=12.042 coef=[ 2.13010188e-01 6.04856163e-02 3.94570854e-02 -1.45835673e-02
2.02363804e-04 1.80238012e-02]
k=32 iter=65 loss=10.417 coef=[ 0.21465458 0.0601092 0.03948894 -0.00942473 0.00031827 0.01066371]
k=33 iter=83 loss=7.794 coef=[ 0.2142561 0.05964649 0.03965735 -0.00620213 0.00060021 0. ]
k=34 iter=58 loss=7.209 coef=[ 2.14882482e-01 5.96866299e-02 3.96718697e-02 -7.91501061e-03
1.30921916e-04 2.30951749e-04]
k=35 iter=156 loss=6.490 coef=[ 0.215525 0.05983936 0.03986242 -0.00339554 0.00126157 0. ]
k=36 iter=24 loss=6.100 coef=[ 2.16225711e-01 5.97631920e-02 3.97397925e-02 -2.45147014e-03
2.44985747e-05 3.94253299e-04]
k=37 iter=64 loss=8.129 coef=[2.17145372e-01 6.16970312e-02 3.95198185e-02 0.00000000e+00
3.47273204e-05 3.72053417e-02]
k=38 iter=72 loss=6.293 coef=[ 0.21730507 0.05947258 0.03934373 -0.0133852 0. 0.00212843]
k=39 iter=97 loss=6.289 coef=[ 2.17466481e-01 6.10224959e-02 3.95355674e-02 -2.28704915e-04
1.17821022e-04 2.52429046e-02]
k=40 iter=53 loss=9.932 coef=[ 2.20071058e-01 6.00382635e-02 3.89921300e-02 -1.60171344e-02
3.21467173e-06 1.77326300e-02]
k=41 iter=30 loss=8.583 coef=[ 2.20182668e-01 5.97374142e-02 3.90873653e-02 -2.09566241e-02
2.88851288e-06 1.10818734e-02]
k=42 iter=47 loss=4.073 coef=[ 2.19054761e-01 6.01020482e-02 3.96473356e-02 -7.12168506e-03
1.47716932e-04 7.69246767e-03]
k=43 iter=89 loss=5.757 coef=[ 0.21974316 0.06084389 0.03931738 -0.00528931 0. 0.02585219]
k=44 iter=40 loss=8.442 coef=[ 2.21560982e-01 6.04808130e-02 3.89569009e-02 -1.22486407e-02
3.29704333e-05 2.59377010e-02]
k=45 iter=46 loss=4.993 coef=[ 0.2215624 0.06100362 0.03960818 -0.00686819 0.00096912 0.02399588]
k=46 iter=68 loss=6.433 coef=[ 0.22201089 0.06091556 0.03907551 -0.00679388 0.0015962 0.03213174]
k=47 iter=48 loss=3.324 coef=[ 0.22136523 0.05975528 0.03951702 -0.0159408 0.00278059 0.00496304]
k=48 iter=86 loss=3.519 coef=[ 0.22152836 0.05984184 0.03947445 -0.01612191 0.00418253 0.00764482]
k=49 iter=66 loss=3.440 coef=[ 0.222211 0.05994794 0.03918111 -0.01243255 0.00334225 0.01413317]
k=50 iter=55 loss=4.113 coef=[ 2.23966419e-01 5.99711842e-02 3.94033541e-02 -2.09409822e-02
1.98243210e-06 9.61521648e-03]
k=51 iter=77 loss=1.871 coef=[ 0.2217757 0.05943839 0.0392259 -0.01556521 0.0089571 0.00661485]
k=52 iter=23 loss=2.395 coef=[ 0.22286991 0.06037014 0.03949072 -0.01110128 0.00298821 0.0159151 ]
k=53 iter=90 loss=1.655 coef=[ 0.22185925 0.05985215 0.03914311 -0.01111838 0.01009708 0.01546789]
k=54 iter=15 loss=1.553 coef=[ 0.22355758 0.06010778 0.03938089 -0.00976235 0.00225962 0.0127162 ]
k=55 iter=135 loss=1.082 coef=[ 0.22062266 0.05905764 0.03898353 -0.0194163 0.01728448 0.0070784 ]
k=56 iter=104 loss=1.198 coef=[ 0.22226256 0.05984474 0.03918067 -0.01321531 0.01086554 0.01497301]
k=57 iter=87 loss=1.488 coef=[ 0.22337306 0.06064525 0.03928315 -0.00652562 0.00818666 0.0259949 ]
k=58 iter=171 loss=1.555 coef=[ 0.22040376 0.05892565 0.03858353 -0.02690285 0.02307313 0.01370072]
k=59 iter=17 loss=1.296 coef=[ 0.22562796 0.06058376 0.03957689 -0.01117352 0.00092516 0.01770546]
k=60 iter=108 loss=1.690 coef=[ 0.2241568 0.06051196 0.03911443 -0.01351868 0.00939518 0.02707935]
k=61 iter=59 loss=1.964 coef=[ 0.22584375 0.06117987 0.03923742 -0.00747088 0.00380839 0.03439573]
k=62 iter=29 loss=2.123 coef=[ 0.22699276 0.06060142 0.03932837 -0.02177034 0.00088479 0.02194526]
k=63 iter=52 loss=2.251 coef=[ 0.2270644 0.06063761 0.03923185 -0.02395359 0.00235248 0.0247866 ]
k=64 iter=73 loss=2.240 coef=[ 0.2269509 0.06028926 0.03914241 -0.03200739 0.00363902 0.02084823]
k=65 iter=97 loss=2.549 coef=[ 0.22713774 0.06045412 0.03900066 -0.03416723 0.0055969 0.02688397]
k=66 iter=47 loss=2.771 coef=[ 0.22883137 0.06062405 0.03910661 -0.03708888 0.00080515 0.02627998]
k=67 iter=50 loss=2.693 coef=[ 0.22949555 0.06067264 0.03910994 -0.03909611 0.00050112 0.02695274]
k=68 iter=42 loss=0.924 coef=[ 2.28574397e-01 6.12937273e-02 3.95076224e-02 -7.66211637e-03
2.58341294e-05 3.02536220e-02]
k=69 iter=57 loss=1.872 coef=[ 2.30103554e-01 6.07790211e-02 3.92372360e-02 -3.49647974e-02
1.26867389e-04 2.63625512e-02]
k=70 iter=63 loss=1.559 coef=[ 2.30588671e-01 6.07916566e-02 3.93136053e-02 -3.34340256e-02
4.38694386e-05 2.51822088e-02]
k=71 iter=69 loss=1.142 coef=[ 2.30638931e-01 6.08634712e-02 3.94238642e-02 -2.75580307e-02
4.49739709e-06 2.44281604e-02]
k=72 iter=76 loss=0.928 coef=[ 0.23103192 0.06082811 0.03951699 -0.02599048 0. 0.02218113]
k=73 iter=80 loss=0.709 coef=[ 0.23108334 0.06099315 0.03959114 -0.0186504 0. 0.02365333]
k=74 iter=91 loss=0.763 coef=[ 0.23224842 0.06082253 0.03964384 -0.02437628 0. 0.01985456]
k=75 iter=120 loss=1.783 coef=[ 2.34585125e-01 6.15769341e-02 3.91393427e-02 -3.98933333e-02
2.65355112e-06 4.17771345e-02]
k=76 iter=102 loss=0.605 coef=[ 0.23293707 0.0613851 0.03976459 -0.01016956 0. 0.02720179]
k=77 iter=152 loss=2.097 coef=[ 2.37444147e-01 6.21706274e-02 3.90139316e-02 -4.26876400e-02
1.50369021e-07 5.43312502e-02]
k=78 iter=104 loss=0.399 coef=[ 0.23279685 0.06061006 0.04018587 -0.00582862 0. 0.00703342]
k=79 iter=119 loss=0.544 coef=[ 0.23451724 0.06070914 0.04023867 -0.00771722 0. 0.00778842]
k=80 iter=194 loss=1.022 coef=[ 0.23861323 0.06139807 0.03972772 -0.03213913 0. 0.02806008]
Résumé
dfcoef = pandas.DataFrame(coefs).set_index('k')
dfcoef
On visualise.
with warnings.catch_warnings():
warnings.simplefilter("ignore", DeprecationWarning)
fig, ax = plt.subplots(2, 3, figsize=(14, 6))
dfcoef[["mu", "nu"]].plot(ax=ax[0, 0], logy=True)
dfcoef[["beta"]].plot(ax=ax[0, 1], logy=True)
dfcoef[["loss"]].plot(ax=ax[1, 0], logy=True)
dfcoef[["R0"]].plot(ax=ax[0, 2])
df.plot(ax=ax[1, 1], logy=True)
fig.suptitle('Estimation de R0 tout au long de la simulation', fontsize=12)
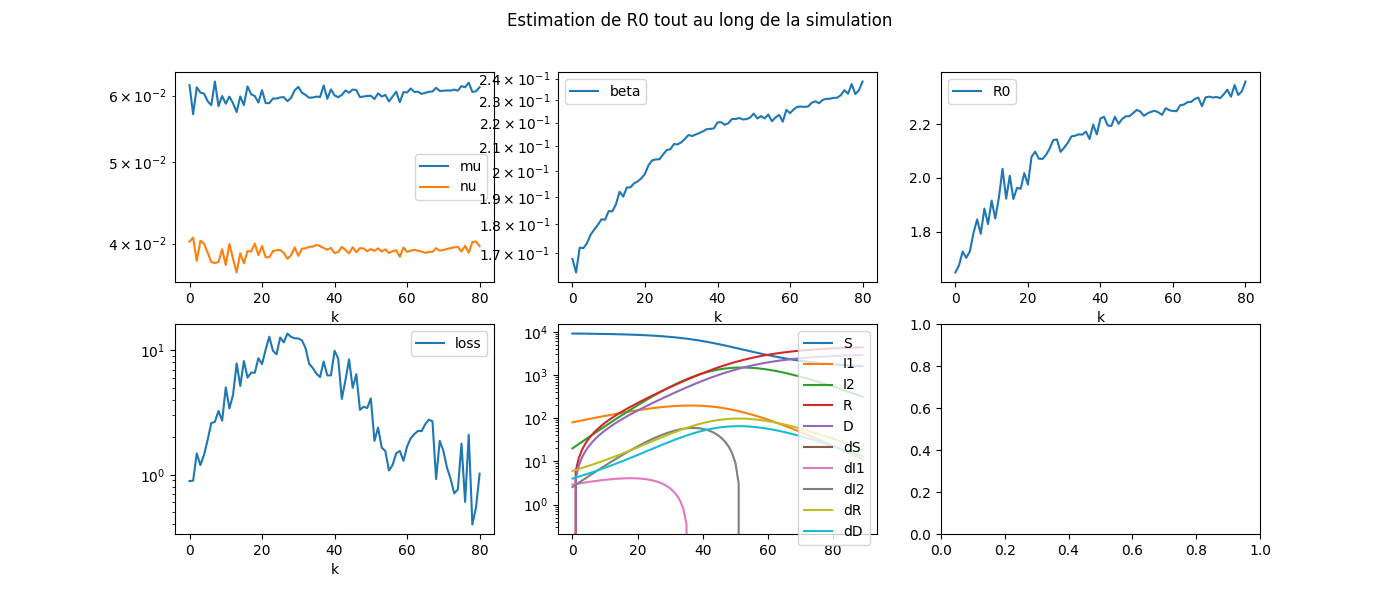
Total running time of the script: ( 2 minutes 5.775 seconds)
