2A.ML101.4: Supervised Learning: Regression

Links: notebook, html, python, slides, GitHub

Here we’ll do a short example of a regression problem: learning a continuous value from a set of features.

The question is: can you predict the progression of the disease?

Source: Course on machine learning with scikit-learn by Gaël Varoquaux

from sklearn.datasets import load_diabetes
data = load_diabetes()
print(data.data.shape)
print(data.target.shape)

(442, 10)
(442,)

We can see that there are just over 440 data points.

The DESCR variable has a long description of the dataset:

print(data.DESCR)

.. _diabetes_dataset:
Diabetes dataset
----------------
Ten baseline variables, age, sex, body mass index, average blood
pressure, and six blood serum measurements were obtained for each of n =
442 diabetes patients, as well as the response of interest, a
quantitative measure of disease progression one year after baseline.
Data Set Characteristics:
  :Number of Instances: 442
  :Number of Attributes: First 10 columns are numeric predictive values
  :Target: Column 11 is a quantitative measure of disease progression one year after baseline
  :Attribute Information:
      - age     age in years
      - sex
      - bmi     body mass index
      - bp      average blood pressure
      - s1      tc, total serum cholesterol
      - s2      ldl, low-density lipoproteins
      - s3      hdl, high-density lipoproteins
      - s4      tch, total cholesterol / HDL
      - s5      ltg, possibly log of serum triglycerides level
      - s6      glu, blood sugar level
Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times the square root of n_samples (i.e. the sum of squares of each column totals 1).
Source URL:
https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html
For more information see:
Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.
(https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)

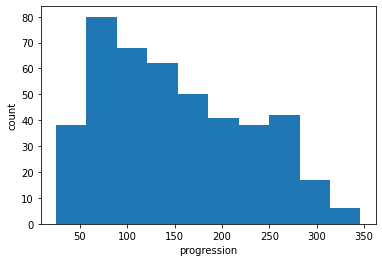
It often helps to quickly visualize pieces of the data using histograms, scatter plots, or other plot types. Here we’ll load pylab and show a histogram of the target values: the median price in each neighborhood.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

plt.hist(data.target)
plt.xlabel('progression')
plt.ylabel('count');

Let’s have a quick look to see if some features are more relevant than others for our problem

for index, feature_name in enumerate(data.feature_names):
    plt.figure()
    plt.scatter(data.data[:, index], data.target)
    plt.ylabel('Progression')
    plt.xlabel(feature_name)

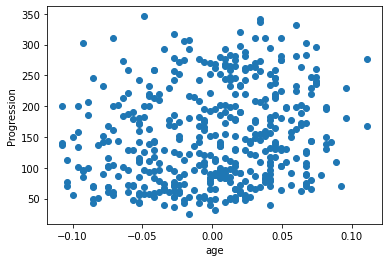
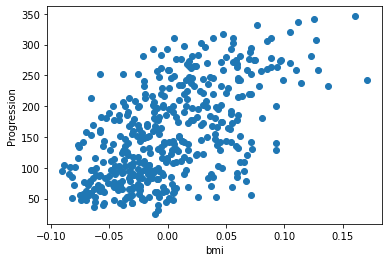
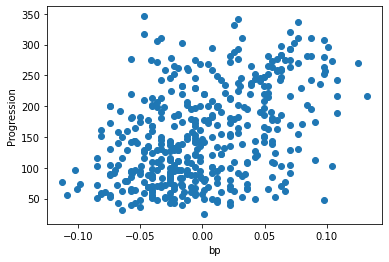
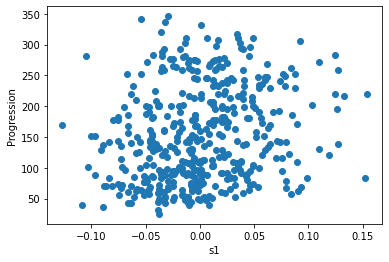
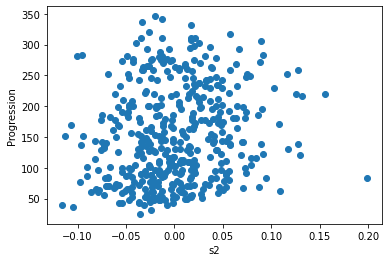
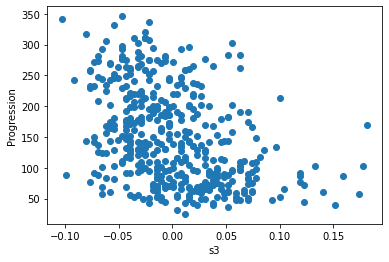
This is a manual version of a technique called feature selection.

Sometimes, in Machine Learning it is useful to use feature selection to decide which features are most useful for a particular problem. Automated methods exist which quantify this sort of exercise of choosing the most informative features.

Predicting Progression: a Simple Linear Regression

Now we’ll use scikit-learn to perform a simple linear regression on the housing data. There are many possibilities of regressors to use. A particularly simple one is LinearRegression: this is basically a wrapper around an ordinary least squares calculation.

We’ll set it up like this:

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(data.data, data.target)

from sklearn.linear_model import LinearRegression

clf = LinearRegression()
clf.fit(X_train, y_train)

LinearRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

predicted = clf.predict(X_test)
expected = y_test

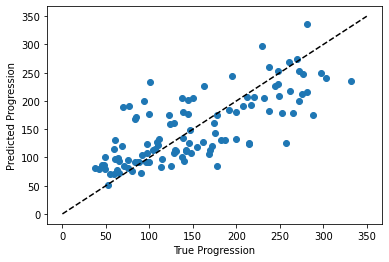
plt.scatter(expected, predicted)
plt.plot([0, 350], [0, 350], '--k')
plt.axis('tight')
plt.xlabel('True Progression')
plt.ylabel('Predicted Progression')
print("RMS:", np.sqrt(np.mean((predicted - expected) ** 2)))

RMS: 46.2788680281883

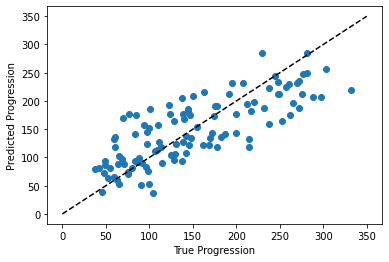
The prediction at least correlates with the true price, though there are clearly some biases. We could imagine evaluating the performance of the regressor by, say, computing the RMS residuals between the true and predicted price. There are some subtleties in this, however, which we’ll cover in a later section.

Exercise: Gradient Boosting Tree Regression

There are many other types of regressors available in scikit-learn: we’ll try a more powerful one here.

Use the GradientBoostingRegressor class to fit the data.

You can copy and paste some of the above code, replacing LinearRegression with GradientBoostingRegressor.

from sklearn.ensemble import GradientBoostingRegressor
# Instantiate the model, fit the results, and scatter in vs. out

Solution:

from sklearn.ensemble import GradientBoostingRegressor

clf = GradientBoostingRegressor()
clf.fit(X_train, y_train)

predicted = clf.predict(X_test)
expected = y_test

plt.scatter(expected, predicted)
plt.plot([0, 350], [0, 350], '--k')
plt.axis('tight')
plt.xlabel('True Progression')
plt.ylabel('Predicted Progression')
print("RMS:", np.sqrt(np.mean((predicted - expected) ** 2)))

RMS: 50.35162346769333