2A.ml - Problèmes classiques de machine learning illustrés#

Links: notebook, html, python, slides, GitHub

Revue des problèmes classiques de machines learning, classification, régression, ranking. Exercices sur la classification multi-classes.

from jyquickhelper import add_notebook_menu
add_notebook_menu(last_level=3)

%matplotlib inline
import matplotlib.pyplot as plt

Dans les exemples qui suivent :

$e(X,Y)$ est une fonction d’erreur
$\Theta$ et un jeu de coefficients
$f(\Theta, X_i)$ la prédiction pour l’observation $i$ , $\Theta$ représente les paramètres
$(X_i, Y_i)$ est un jeu de données

Note

Les exemples suivants ne divisent pas les données en base d’apprentissage / base de test. Les modèles sont appris et testés sur les mêmes données ce qu’on ne fait jamais en pratique mais cela permet de voir précisément ce que le modèle apprend. La résolution des problèmes d’optimisation suppose que les données sont homogènes (elles suivent la même lois) et indépendantes.

Supervisés #

Regression #

add_notebook_menu(menu_id="reg", first_level=3, last_level=4, keep_item=0)

données #

$(X_i, Y_i)$ , avec $X_i \in \mathbb{R}^n$ et $Y_i \in \mathbb{R}$ .

sortie #

$\hat{Y_i} \in \mathbb{R}$ , $\hat{Y_i} = f(\Theta, X_i)$

optimisation #

$\min_\Theta \sum_i e(Y_i, f(\Theta, X_i))$

Dans le cas standard, la fonction d’erreur est quadratique : $\min_\Theta \sum_i (Y_i - f(\Theta, X_i))^2$ et correspond au problème de modélisation $Y \sim f(\Theta, X_i) + \epsilon$ avec $\epsilon$ bruit gaussien.

évaluation #

$r^2 = 1 - \frac{ \sum_i (Y_i - f(\Theta, X_i))^2 } { \sum_i (Y_i - \bar{Y})^2 } \leqslant 1 \text{ ou } 1 - \frac{ \sum_i e(Y_i, f(\Theta, X_i) } { \sum_i e(Y_i, \hat{Y}) }$

exemple #

import numpy.random
X = numpy.random.random((100, 1))
xx = numpy.random.normal(size=(100, 1)) / 10
Y = X*X + xx

fig, ax = plt.subplots()
ax.plot(X, Y, ".", label="data")
ax.legend()
ax.set_title("Courbe façon nuage de points");

../_images/ml_c_machine_learning_problems_13_0.png

On compare deux modèles, une régression linéaire et un arbre de décision.

# model 1
from sklearn.linear_model import LinearRegression
clr = LinearRegression()
clr.fit(X, Y)
Yp = clr.predict(X)

# model 2
from sklearn.tree import DecisionTreeRegressor
clr2 = DecisionTreeRegressor(max_depth=4)
clr2.fit(X, Y)
Yp2 = clr2.predict(X)

fig, ax = plt.subplots()
ax.plot(X, Y, ".", label="data")
ax.plot(X, Yp, ".", label="model 1")
ax.plot(X, Yp2, "g.", label="model 2")
ax.legend()
ax.set_title("Régressions linéaires");

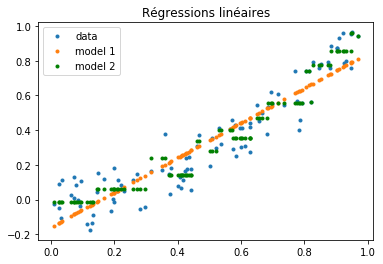
../_images/ml_c_machine_learning_problems_17_0.png

graphe erreur XY #

fig, ax = plt.subplots()
ax.plot(Y, Yp, ".", label="model 1")
ax.plot(Y, Yp2, "g.", label="model 2")
mm = [numpy.min(Y), numpy.max(Y)]
ax.plot(mm, mm,"--")
ax.set_xlabel("Y attendu")
ax.set_ylabel("Y prédit")
ax.legend()
ax.set_title("Régression linéaire");

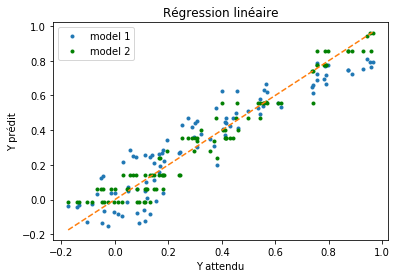
../_images/ml_c_machine_learning_problems_19_0.png

Plus ce nuage est confondu avec la droite, plus il est performant. S’il y a trop de points, on peut trier les erreurs par ordre croissant :

err1 = ((Y - Yp)).reshape((len(Y),))
err1.sort()
err2 = ((Y - Yp2.reshape((len(Y), 1)))).reshape((len(Y),))
err2.sort()

fig, ax = plt.subplots()
ax.plot(err1, label="model 1")
ax.plot(err2, label="model 2")
ax.set_xlabel("observations")
ax.set_ylabel("erreur")
ax.set_title("Répartition des erreurs");

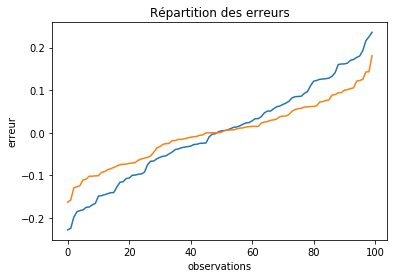
../_images/ml_c_machine_learning_problems_22_0.png

L’erreur correspond alors à l’aire sous la courbe.

Classification binaire #

add_notebook_menu(menu_id="classif", first_level=3, last_level=4, keep_item=1)

données #

$(X_i, Y_i)$ , avec $X_i \in \mathbb{R}^n$ et $Y_i \in \{0,1\}$ .

sortie #

$(c_i, p_i^c)$ avec $c_i \in \{0,1\}$ la classe prédite et $p_i^c \in [0,1]$ la probabilité d’appartenance à la classe $c$ ou score de confiance. $p_i^1 = f(\Theta, X_i)$ et $p_i^0 = 1 - p_i^1$ .

optimisation #

Le problème d’optimisation dépend du modèle. On note $f(\Theta,X_i) = P(Y=1 | X_i, \Theta)$ , la probabilité que $X$ appartienne la la classe 1.

régression logistique

On optimise la vraisemblance déterminée par $\ln L(\Theta,X,Y) = \sum_i Y_i \ln f(\Theta,X_i) + (1-Y_i) \ln(1-f(\Theta,X_i))$ .

arbre

On écrit rarement le critère à optimiser pour l’arbre dans sa totalité mais seulement pour une feuille de l’arbre qu’on cherche à découper. On optimise une métrique (Gini, entropie, variance). Si on note $f(k)$ la proportion d’éléments bien classés par cette feuille. Le critère optimisé est : $-\sum_k f(k)\ln f(k)$ .

from pyquickhelper.helpgen import NbImage
NbImage("dt.png", width=600)

../_images/ml_c_machine_learning_problems_29_0.png

La pertinence de la division d’un noeud de l’arbre consiste à trouver un seuil de coupure pour une variable qui diminue le critère d’impureté $I$ . Dans le cas de cette arbre :

$\begin{array}{rcl}\Delta I &=& I(noeud \; parent) - I(noeud \; fils \; gauche) - I(noeud \; fils \; droit) \\ &=& - (0.64 \ln 0.64 + 0.36 \ln 0.36) + (0.4 \ln 0.4 + 0.6 \ln 0.6) + 0 \\ &=& -0.019 \end{array}$

évaluation #

exemple #

import numpy.random
X = numpy.random.normal(size=(100, 2))
Y = numpy.random.randint(2, size=(100, ))
X[Y==1,0] += 1.2
X[Y==1,1] += 1.2

fix, ax = plt.subplots()
ax.plot(X[Y==0,0], X[Y==0,1], "o")
ax.plot(X[Y==1,0], X[Y==1,1], "o")
ax.set_title("Nuage de points avec deux classes");

../_images/ml_c_machine_learning_problems_34_0.png

# model 1
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression()
clf.fit(X, Y)
Yp = clf.predict(X)

# model 1
from sklearn.tree import DecisionTreeClassifier
clf2 = DecisionTreeClassifier(max_depth=3)
clf2.fit(X, Y)
Yp2 = clf2.predict(X)

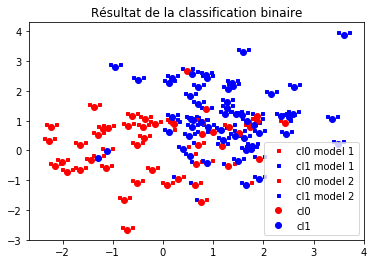
fig, ax = plt.subplots()
ax.plot(X[Yp==0,0]+0.1, X[Yp==0,1]+0.1, "rs", label="cl0 model 1", ms=3)
ax.plot(X[Yp==1,0]+0.1, X[Yp==1,1]+0.1, "bs", label="cl1 model 1", ms=3)
ax.plot(X[Yp2==0,0]-0.1, X[Yp2==0,1]+0.1, "rs", label="cl0 model 2", ms=3)
ax.plot(X[Yp2==1,0]-0.1, X[Yp2==1,1]+0.1, "bs", label="cl1 model 2", ms=3)
ax.plot(X[Y==0,0], X[Y==0,1], "ro", label="cl0")
ax.plot(X[Y==1,0], X[Y==1,1], "bo", label="cl1")
ax.legend()
ax.set_title("Résultat de la classification binaire");

../_images/ml_c_machine_learning_problems_37_0.png

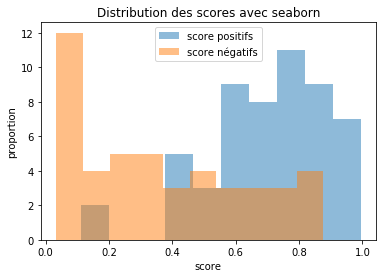
distribution des scores #

from sklearn.metrics import roc_curve, auc

Ypr = clf.predict_proba(X)

score_pos = Ypr[Y == 1, 1]
score_neg = Ypr[Y == 0, 1]

import numpy
numpy.average(score_neg), numpy.average(score_pos)

(0.36854464309856544, 0.7010128988674563)

On utilise seaborn.

f, ax = plt.subplots()
ax.hist(score_pos, label="score positifs", alpha=0.5)
ax.hist(score_neg, label="score négatifs", alpha=0.5)
ax.set_xlabel("score")
ax.set_ylabel("proportion")
ax.legend()
ax.set_title("Distribution des scores avec seaborn");

../_images/ml_c_machine_learning_problems_43_0.png

graphe erreur ROC #

Courbe ROC

from sklearn.metrics import roc_curve, auc

# model 1
Ypr = clf.predict_proba(X)
fpr, tpr, thresholds = roc_curve(Y, Ypr[:,1]) # on choisit la classe 1

# model 2
Ypr2 = clf2.predict_proba(X)
fpr2, tpr2, thresholds2 = roc_curve(Y, Ypr2[:,1]) # on choisit la classe 1

auc(fpr, tpr), auc(fpr2, tpr2)

(0.8337359098228664, 0.8836553945249597)

import pandas
df = pandas.DataFrame({"seuil":thresholds, "fpr":fpr, "tpr": tpr })[["seuil", "fpr", "tpr"]]
pandas.concat([df.head(), df.tail()])

	seuil	fpr	tpr
0	0.994020	0.000000	0.018519
1	0.878538	0.000000	0.203704
2	0.876186	0.021739	0.203704
3	0.844416	0.021739	0.277778
4	0.837452	0.043478	0.277778
28	0.166698	0.739130	0.962963
29	0.143926	0.739130	0.981481
30	0.111130	0.782609	0.981481
31	0.110802	0.782609	1.000000
32	0.032959	1.000000	1.000000

fix, ax = plt.subplots()
ax.plot(fpr, tpr, ".-", label="model 1 auc=%0.2f" % auc(fpr, tpr))
ax.plot(fpr2, tpr2, ".-", label="model 2 auc=%0.2f" % auc(fpr2, tpr2))
ax.set_xlabel("FPR = False Positive Rate")
ax.set_ylabel("TPR = True Positive Rate")
ax.legend()
ax.set_title("Courbe ROC");

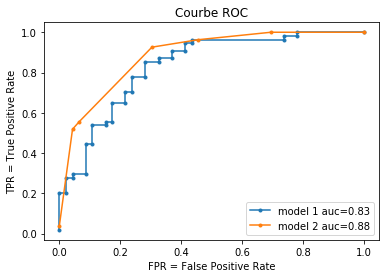
../_images/ml_c_machine_learning_problems_49_0.png

La courbe ROC est définie par l’ensemble des points $(FPR(s), TPR(s))$ pour $s \in [0,1]$ . Le score de classification désigne le score de la classe de classification dans la classe 1. Pour un seuil $s$ , on note:

$P(s)$ est l’ensemble des observations pour lesquelles le score de classification est supérieur à $s$ et la réponse attendue est 1
$N(s)$ est l’ensemble des observations pour lesquelles le score de classification est supérieur à $s$ et la réponse attendue est 0
$TP(s)$ est l’ensemble des observations pour lesquelles le score de classification est supérieur à $s$ et la prédiction est 1 et la classe attendue est 1
$FN(s)$ est l’ensemble des observations pour lesquelles le score de classification est supérieur à $s$ et la prédiction est 0 et la classe attendue 0

$FPR(s) = \frac{ FN(s) }{ N(s)}$ et $TPR(s) = \frac{ TP(s) }{ P(s)}$

graphe frontière #

Si le nombre de features est supérieur à 2, il faut appliquer une ACP pour réduire les dimmensions.

# nuage de points
from matplotlib.colors import ListedColormap
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])

fig, ax = plt.subplots()

# grille
h = .02
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = numpy.meshgrid(numpy.arange(x_min, x_max, h),
                        numpy.arange(y_min, y_max, h))

# valeur pour cette grille
if hasattr(clf, "decision_function"):
    Z = clf.decision_function(numpy.c_[xx.ravel(), yy.ravel()])
else:
    Z = clf.predict_proba(numpy.c_[xx.ravel(), yy.ravel()])[:, 1]

#
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, cmap=cm, alpha=.8)
ax.scatter(X[:, 0], X[:, 1], c=Y, cmap=cm_bright)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_title("Utilisation de la couleur pour\nreprésenter les scores");

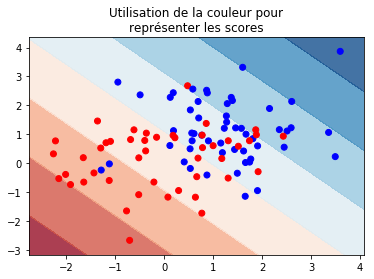
../_images/ml_c_machine_learning_problems_52_0.png

# nuage de points
from matplotlib.colors import ListedColormap
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])

fig, ax = plt.subplots()

# grille
h = .02
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = numpy.meshgrid(numpy.arange(x_min, x_max, h),
                        numpy.arange(y_min, y_max, h))

# valeur pour cette grille
if hasattr(clf2, "decision_function"):
    Z = clf2.decision_function(numpy.c_[xx.ravel(), yy.ravel()])
else:
    Z = clf2.predict_proba(numpy.c_[xx.ravel(), yy.ravel()])[:, 1]

#
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, cmap=cm, alpha=.8)
ax.scatter(X[:, 0], X[:, 1], c=Y, cmap=cm_bright)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_title("Couleur, score et arbres");

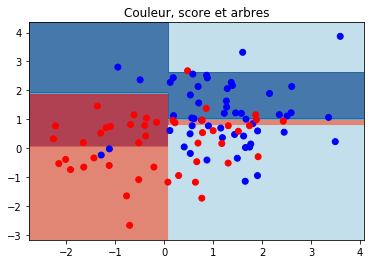
../_images/ml_c_machine_learning_problems_53_0.png

matrice de confusion #

from sklearn.metrics import confusion_matrix
confusion_matrix(Y, Yp)

array([[31, 15],
       [ 7, 47]], dtype=int64)

confusion_matrix(Y, Yp2)

array([[32, 14],
       [ 4, 50]], dtype=int64)

Plusieurs dimensions #

Régression #

$Y_i \in \mathbb{Y^p}$

Addition des erreurs sur les différentes dimensions

Classification #

$Y_i \in E$ où $E$ est un ensemble sur lequel il n’y a pas de relation d’ordre.

On transforme le problème en plusieurs problèmes de classification binaire.

Ranking #

add_notebook_menu(menu_id="rank", first_level=3, last_level=4, keep_item=3)

données #

$(G_i, X_i, Y_i)$ , avec $X_i \in \mathbb{R}$ et $Y_i \in \mathbb{N}$ .

$G_i$ est un identifiant qui permet de regroupes les observations ensemble. Au sein d’un groupe, $Y_i$ détermine l’ordre dans lequel les observations doivent être triées.

sortie #

$S_i$ , ce score permet de trier les observations au sein d’un groupe.

optimisation #

Deux approches :

score : on émet l’hypothèse qu’il existe un score qui permet de trier les éléments entre eux, la connaissance du groupe $G_i$ est superflu, le problème de ranking devient un problème de régression où on cherche à apprendre le score.
pair-wise : le score n’est pas connu, tout ce qu’on sait faire est d’exprimer une préférence entre les éléments $(G_i=g,X_i)$ et $(G_j=g,X_j)$ . On transforme le problème le problème de ranking en un problème de classification binaire, pour chaque chaque pair d’oboservations au sein du même groupe, on aprend la préférence.

évaluation #

corrélation entre les positions attendues et prédites au sein du même groupe d’observations

Non supervisés #

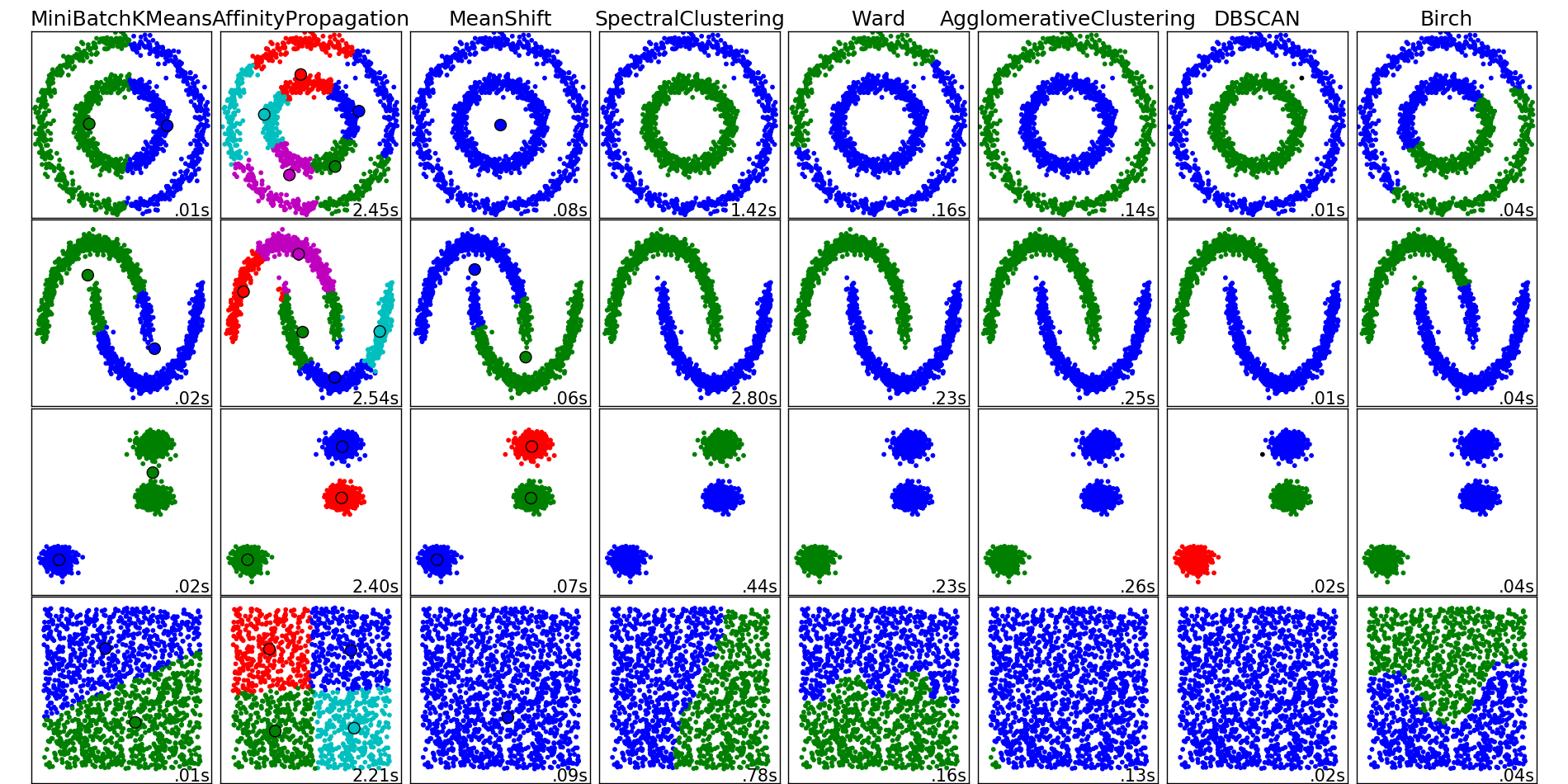
Clustering #

Principales différences entre algorithmes :

espace veectoriel / espace métrique (distance uniquement)
nombre de clusters fixés à l’avance ou déterminé en cours de route
coût

from pyquickhelper.helpgen import NbImage
NbImage("sphx_glr_plot_cluster_comparison_001.png")

../_images/ml_c_machine_learning_problems_70_0.png

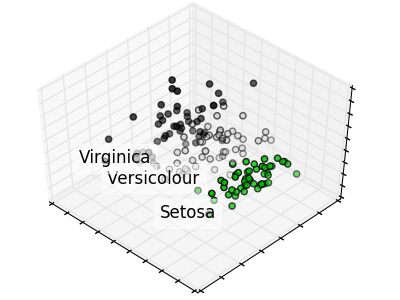
Réduction de dimensions #

NbImage("sphx_glr_plot_pca_iris_001.png")

../_images/ml_c_machine_learning_problems_72_0.png

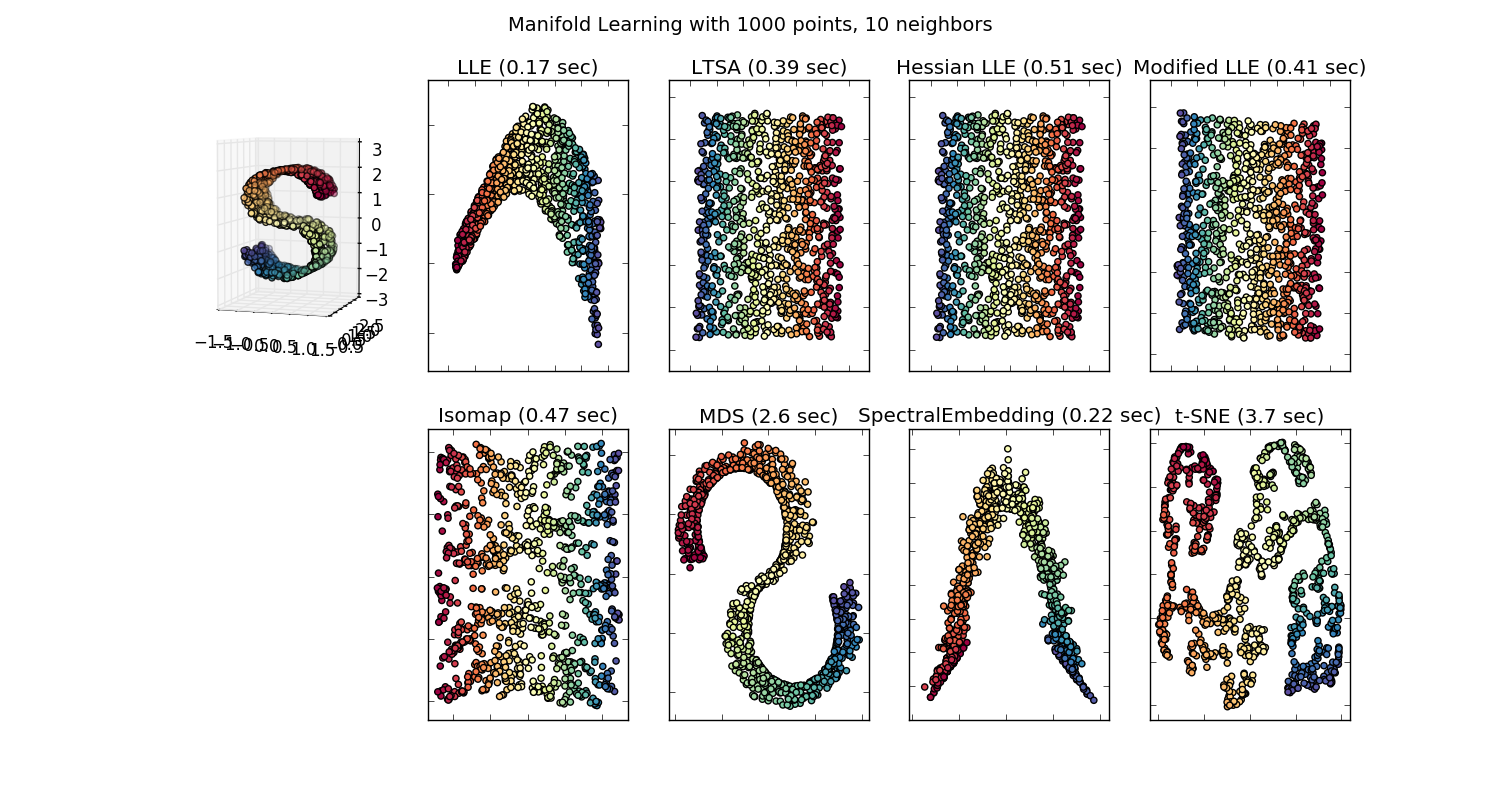
NbImage("sphx_glr_plot_compare_methods_001.png")

../_images/ml_c_machine_learning_problems_73_0.png

Ridge / Lasso / Régularisation #

Ces deux méthodes Ridge et Lasso ont été développés pour ces modèles linéaires. On retrouve des idées similaires pour l’optimisation d’autres modèles en particulier Ridge qui revient à ajouter une pénalité de régularisation des coefficients lors de l’apprentissage. C’est le cas du paramètre alpha qui apparaît lorsqu’on définit un réseau de neurones avec scikit-learn.

Learner / Transformer / Pipeline #

Le module scikit-learn fait apparaître le terme de transformeur : StandardScaler est un transformeur (ou transformer en anglais). Ce type d’objet transforme les données mais ne produisent le résultat final. Un Pipeline empile une liste de transformeurs et un estimateur final (classifieur, régresseur). Une ACP est un transformeur car elle modifie les entrées $X$ avant un apprentissage.

from pyquickhelper.helpgen import NbImage
NbImage("pipeline.png")

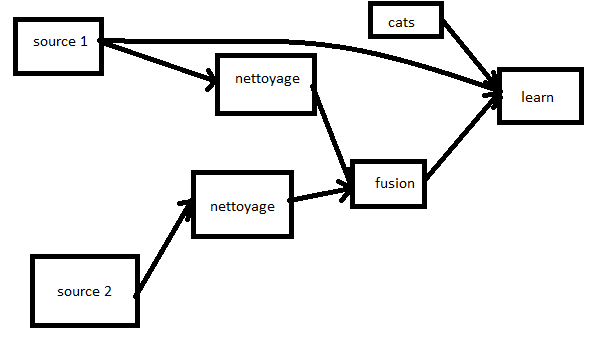
../_images/ml_c_machine_learning_problems_76_0.png

Un pipeline simple :

from sklearn.datasets import load_iris
data = load_iris()
X = data.data
Y = data.target

from sklearn.pipeline import Pipeline
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
pipe = Pipeline([("acp", PCA()),
                 ("logreg", LogisticRegression())])
pipe.fit(X, Y)

Pipeline(memory=None,
     steps=[('acp', PCA(copy=True, iterated_power='auto', n_components=None, random_state=None,
  svd_solver='auto', tol=0.0, whiten=False)), ('logreg', LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
          verbose=0, warm_start=False))])

pred = pipe.predict(X)
pred[:5]

array([0, 0, 0, 0, 0])

Lors de la prédiction, les variables passent par la même chaîne de traitement. Les méthodes pour les transformer et estimator sont différents :

estimator : fit + predict
transformer : fit (optionnel) + transform

La méthode fit ne s’applique pas à tous les transformers. Il n’y a pas toujours de coefficients à estimer. La plupart des transformer sont non supervisés (pas besoin de Y) mais certains le sont comme t-SNE.

Exercice 1 : classifier avec plusieurs classes #

La plupart des modèles ne savant pas gérer le cas multi-class, seulement le cas de la classification binaire.

One vs Rest
One vs One
Et si on transformait le label en une variable…

Il faut comparer ces trois approches.

Exercice 2 : grand nombre de classes ?#

Pourquoi un grand nombre de classes aboutit-il nécessairement à un cas de jeu de données imbalanced ? Que proposez-vous pour y remédier ?

Exercice 3 : ranking #

Résoudre un problème de ranking.

Liens

Contenu

Information

Sujet précédent

Sujet suivant

2A.ml - Problèmes classiques de machine learning illustrés#

Supervisés #

Regression #

données #

sortie #

optimisation #

évaluation #

exemple #

graphe erreur XY #

Classification binaire #

données #

sortie #

optimisation #

évaluation #

exemple #

distribution des scores #

graphe erreur ROC #

graphe frontière #

matrice de confusion #

Plusieurs dimensions #

Régression #

Classification #

Ranking #

données #

sortie #

optimisation #

évaluation #

Non supervisés #

Clustering #

Réduction de dimensions #

Ridge / Lasso / Régularisation #

Learner / Transformer / Pipeline #

Exercice 1 : classifier avec plusieurs classes #

Exercice 2 : grand nombre de classes ?#

Exercice 3 : ranking #