1A.1 - Tracer une pyramide bigarrée - correction#

Links: notebook, html, python, slides, GitHub

Cet exercice est inspirée de l’article 2015-04-07 Motif, optimisation, biodiversité. Il s’agit de dessiner un motif. Correction.

from jyquickhelper import add_notebook_menu
add_notebook_menu()

%matplotlib inline

Problème#

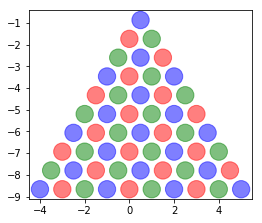
Il s’agit de dessiner la pyramide suivante à l’aide de matplotlib.

from IPython.display import Image
Image("http://www.xavierdupre.fr/app/code_beatrix/helpsphinx/_images/biodiversite_tri2.png")
../_images/td1a_pyramide_bigarree_correction_4_0.png

Idée de la solution#

On sépare le problème en deux plus petits :

  • Trouver la position des boules dans un repère cartésien.

  • Choisir la bonne couleur.

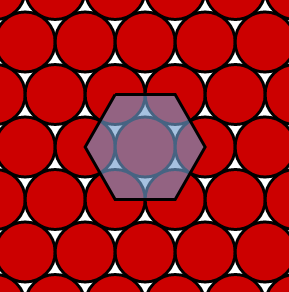
Le repère est hexagonal. L’image suivante est tirée de la page wikipédia empilement compact.

from pyquickhelper.helpgen import NbImage
NbImage("data/hexa.png")
../_images/td1a_pyramide_bigarree_correction_6_0.png

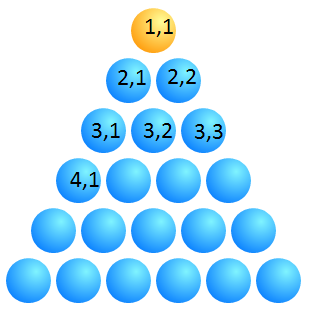
Mais dans un premier temps, il faut un moyen de repérer chaque boule. On les numérote avec deux indices.

Image("http://www.xavierdupre.fr/app/code_beatrix/helpsphinx/_images/pyramide_num2.png")
../_images/td1a_pyramide_bigarree_correction_8_0.png

Les coordonnées#

On prend comme exemple scatter_demo.py sur le site de matplotlib.

import matplotlib.pyplot as plt

fig, ax = plt.subplots(1,1)
n = 10
x = []
y = []
for i in range(1,n+1):
    for j in range(i, n+1):
        x.append(i)
        y.append(j)
size = [300 for c in x]
colors = ["r" for c in x]
ax.scatter(x, y, s=size, c=colors, alpha=0.5)

<matplotlib.collections.PathCollection at 0x193713b3b00>
../_images/td1a_pyramide_bigarree_correction_10_1.png

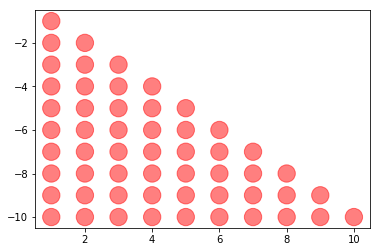
On inverse.

fig, ax = plt.subplots(1,1)
n = 10
x = []
y = []
for i in range(1,n+1):
    for j in range(i, n+1):
        x.append(i)
        y.append(-j)
size = [300 for c in x]
colors = ["r" for c in x]
ax.scatter(x, y, s=size, c=colors, alpha=0.5)

<matplotlib.collections.PathCollection at 0x193714d31d0>
../_images/td1a_pyramide_bigarree_correction_12_1.png

On décale.

fig, ax = plt.subplots(1,1)
n = 10
x = []
y = []
for i in range(1,n+1):
    for j in range(i, n+1):
        x.append(i - j*0.5)
        y.append(-j)
size = [300 for c in x]
colors = ["r" for c in x]
ax.scatter(x, y, s=size, c=colors, alpha=0.5)

<matplotlib.collections.PathCollection at 0x1937155acc0>
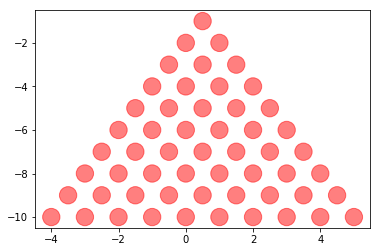
../_images/td1a_pyramide_bigarree_correction_14_1.png

Cela ressemble à de l’hexagonal mais ce n’est pas encore tout à fait cela. La hauteur d’un triangle équilatéral de côté un est \frac{\sqrt{3}}{2}. Ca tombe bien car dans l’exemple précédente, le côté de chaque triangle est 1. Et on change la dimension du graphe tracé avec matplotlib pour éviter de réduire nos effort à néant.

fig, ax = plt.subplots(1,1, figsize=(4, 4*(3**0.5)/2))
n = 10
x = []
y = []
for i in range(1,n+1):
    for j in range(i, n+1):
        x.append(i - j*0.5)
        y.append(-j*(3**0.5)/2)
size = [300 for c in x]
colors = ["r" for c in x]
ax.scatter(x, y, s=size, c=colors, alpha=0.5)

<matplotlib.collections.PathCollection at 0x193718effd0>
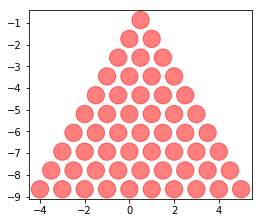
../_images/td1a_pyramide_bigarree_correction_16_1.png

La couleur#

Je vous laisse retourner sur les deux premières images et observer la couleur de toutes les boules qui vérifient (i+j)%3 == 1.

fig, ax = plt.subplots(1,1, figsize=(4, 4*(3**0.5)/2))
n = 10
x = []
y = []
colors = []
trois = "rgb"
for i in range(1,n+1):
    for j in range(i, n+1):
        x.append(i - j*0.5)
        y.append(-j*(3**0.5)/2)
        colors.append(trois[(i+j) % 3])
size = [300 for c in x]
ax.scatter(x, y, s=size, c=colors, alpha=0.5)

<matplotlib.collections.PathCollection at 0x1937198f6d8>
../_images/td1a_pyramide_bigarree_correction_18_1.png