Définition des réseaux de neurones multi-couches#

Les réseaux de neurones multi-couches (ou perceptrons) définissent une classe de fonctions dont l’intérêt est de pouvoir approcher n’importe quelle fonction continue à support compact (voir théorème sur la densité). Aucun autre type de réseau de neurones ne sera étudié et par la suite, tout réseau de neurones sera considéré comme multi-couches (donc pas les réseau de Kohonen).

Un neurone#

Définition D1 : neurone

Un neurone à p entrées est une fonction f : \R^{p+1} \times \R^p \longrightarrow \R définie par :

  • g : \R \longrightarrow \R

  • W \in \R^{p+1}, W=\pa{w_1,\dots,w_{p+1}}

  • \forall x \in \R^p, \; f\pa{W,x} = g \pa { \sum_{i=1}^{p} w_i x_i + w_{p+1}} avec x = \pa{x_1,\dots,x_p}

Cette définition est inspirée du neurone biologique, les poids jouant le rôle de synapses, le vecteur x celui des entrées et W celui des coefficients ou poids. Le coefficient w_{p+1} est appelé le biais et souvent noté b. La fonction g est appelée fonction de transfert ou fonction de seuil.

Figure F1 : neurone graphique

\begin{picture}(100,80)(0,0) \put(10,0) {\circle{20}} \put(10,25) {\circle{20}} \put(10,50) {\circle{20}} \put(10,0) {\makebox(3,3){$x_1$}} \put(10,25) {\makebox(3,3){$x_i$}} \put(10,50) {\makebox(3,3){$x_p$}} \put(80,25) {\circle{35}} \put(78,25) {\makebox(6,3){$\;y \overset{f}{\rightarrow} z$}} \put(20,25) {\line(1,0){43}} \drawline(20,0)(63,25) \drawline(20,50)(63,25) \put(30,50) {\makebox(3,3){$w_p$}} \put(30,18) {\makebox(3,3){$w_i$}} \put(30,-2) {\makebox(3,3){$w_1$}} \put(48,20) {\makebox(3,3){$\sum$}} \put(50,-20) {\circle{20}} \put(50,-20) {\makebox(3,3){$1$}} \drawline(50,-10)(63,25) \put(50,5) {\makebox(3,3){$b$}} \end{picture}

Le vecteur \left( x_1,...,x_p\right) \in \R^p joue le rôle des entrées. y est appelé parfois le potentiel. y=\sum_{i=1}^{p} w_ix_i+b. z est appelée la sortie du neurone. f est appelée la fonction de transfert ou de seuil. z=f \pa{y} = f \pa { \sum_{i=1}^{p} w_ix_i+b }.

La réprésentation graphique est plus souvent celle qu’on retient. Ce schéma est également plus proche de sa définition biologique et dissocie mieux les rôles non symétriques des entrées et des poids. Des exemples de fonctions de transfert sont donnés par la table qui suit. Les plus couramment utilisées sont les fonctions linéaire et sigmoïde.

exemples de fonction de transfert ou de seuil

expression

escalier

1_{\left[ 0,+\infty\right[ }

linéaire

x

sigmoïde entre \cro{0,1}

\dfrac{1}{1+e^{-x}}

sigmoïde entre \cro{-1,1}

1-\dfrac{2}{1+e^{x}}

normale

e^{-\frac{x^{2}}{2}}

exponentielle

e^{x}

relu

x \indicatrice{x \supegal 0}

La plupart des fonctions utilisées sont dérivables et cette propriété s’étend à tout assemblage de neurones, ce qui permet d’utiliser l’algorithme de rétropropagation découvert par [Rumelhart1986]. Ce dernier permet le calcul de la dérivée ouvre ainsi les portes des méthodes d’optimisation basées sur cette propriété. La fonction relu a progressivement remplacé la fonction sigmoïde sur les couches cachées car elle est non linéaire et beaucoup plus rapide à calculer.

Une couche de neurones#

Définition D2 : couche de neurones

Soit p et n deux entiers naturels, on note W \in \R^{n\pa{p+1}} = \pa{W_1,\dots,W_n} avec \forall i \in \intervalle{1}{n}, \; W_i \in \R^{p+1}. Une couche de n neurones et p entrées est une fonction :

F : \R^{n\pa{p+1}} \times \R^p \longrightarrow \R^n

vérfifiant :

  • \forall i \in \intervalle {1}{n}, \; f_i est un neurone.

  • \forall W \in \R^{n\pa{p+1}} \times \R^p, \; F\pa{W,x} = \pa {f_1\pa{W_1,x}, \dots, f_n\pa{W_n,x}}

Une couche de neurones représente la juxtaposition de plusieurs neurones partageant les mêmes entrées mais ayant chacun leur propre vecteur de coefficients et leur propre sortie.

Un réseau de neurones : le perceptron#

Définition D3 : réseau de neurones multi-couches ou perceptron

Un réseau de neurones multi-couches à n sorties, p entrées et C couches est une liste de couches \vecteur{C_1}{C_C} connectées les unes aux autres de telle sorte que :

  • \forall i \in \intervalle {1}{C}, chaque couche C_i possède n_i neurones et p_i entrées

  • \forall i \in \intervalle{1}{C-1}, \; n_i = p_{i+1}, de plus p_1 = p et n_C = n

Les coefficients de la couche C_i sont notés \pa {W_1^i,\dots,W_{n_i}^i}, cette couche définit une fonction F_i. Soit la suite \pa{Z_i}_{0\infegal i \infegal C} définie par :

\begin{array}{l} Z_0 \in \R^p \\ \forall i \in \intervalle{1}{C}, \; Z_i = F_i \pa {W_1^i,\dots,W_{n_i}^i,Z_{i-1}}\end{array}

On pose M = M = \sum_{i=1}^{C}n_i\pa{p_i+1}, le réseau de neurones ainsi défini est une fonction F telle que :

\begin{array}{lrll} F : & \R ^ M \times \R^p & \longrightarrow & \R^n \\ & \pa{W,Z_0} & \longrightarrow & Z_C \end{array}

Figure F2 : Modèle du perceptron multi-couche (multi-layer perceptron, MLP)

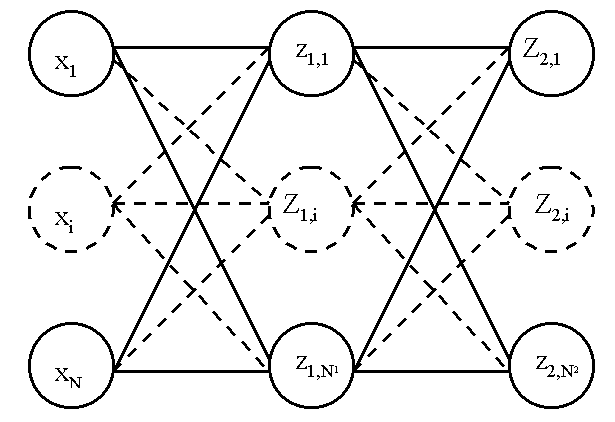
../../_images/rn_gradient.png

  • \vecteur{x_1}{x_p} : entrées

  • C_i nombre de neurones sur la couche i, C_0 = p

  • z_{c,i} sortie du neurone i, de la couche c, par extension, z_{0,i} = x_i

  • y_{c,i} potentiel du neurone i de la couche c

  • w_{c,i,j} coefficient associé à l’entrée j du neurone i de la couche c,

  • b_{c,i} biais du neurone i de la couche c

  • f_{c,i} fonction de seuil du neurone i de la couche c

On note W_c la matrice des poids associée à la couche c. De la même manière, B_c est le vecteur des biais associée à la couche c, Z_c, Y_c sont les objets vectoriels correspondant. On considère que les entrées forment la couche C_0 de manière à simplifier les écritures. Ainsi, chaque couche C_i du perceptron a pour entrées les sorties de la couche C_{i-1}. Cette définition est plus facile à illustrer qu’à énoncer (voir Modèle du perceptron) et rappelle le rôle non symétrique des entrées et des poids. Le mécanisme qui permet de calculer les sorties d’un réseau de neurones sachant ses poids est appelé propagation.

Algorithme A1 : Propagation

Cet algorithme s’applique à un réseau de neurones vérifiant la définition du perceptron. Il s’agit de calculer les sorties de ce réseau connaissant ses poids \pa{w_{c,i,j}} et ses entrées \pa{x_j}.

Z_c \longleftarrow X

Vient ensuite le calcul itératif de la suite \pa{Z_c}_{1 \infegal c \infegal C} :

for c in 1..C :
Y_c \longleftarrow W_c Z_{c-1} + B_c
Z_c \longleftarrow F\pa { Y_c }

Le nombre de couches d’un réseau de neurones n’est pas limité. Les réseaux de deux couches (une couche pour les entrées, une couche de sortie) sont rarement utilisés. Trois couches sont nécessaires (une couche pour les entrées, une couche dite cachée, une couche de sortie) pour construire des modèles avec une propriété intéressante de densité.