Valeurs manquantes et factorisation de matrices#

Links: notebook, html, PDF, python, slides, GitHub

Réflexion autour des valeur manquantes et de la factorisation de matrice positive.

from jyquickhelper import add_notebook_menu
add_notebook_menu()

%matplotlib inline

Matrice à coefficients aléatoires#

On étudie la factorisation d’une matrice à coefficients tout à fait aléatoires qui suivent une loi uniforme sur l’intervalle [0,1]. Essayons sur une petite matrice :

from numpy.random import rand
M = rand(3, 3)
M

array([[ 0.05119593,  0.43722929,  0.9290821 ],
       [ 0.4588466 ,  0.14187813,  0.23762633],
       [ 0.9768084 ,  0.47674026,  0.79044526]])

from sklearn.decomposition import NMF
mf = NMF(1)
mf.fit_transform(M)

array([[ 0.67825803],
       [ 0.38030919],
       [ 1.02295362]])

La matrice précédente est la matrice W dans le produit WH, la matrice qui suit est H.

mf.components_

array([[ 0.73190904,  0.50765757,  0.92611883]])

mf.reconstruction_err_ / (M.shape[0] * M.shape[1])

0.07236890712696428

On recalcule l’erreur :

d = M - mf.fit_transform(M) @ mf.components_
a = d.ravel()
e = a @ a.T
e ** 0.5 / (M.shape[0] * M.shape[1])

0.072368907126964283

e.ravel()

array([ 0.42421796])

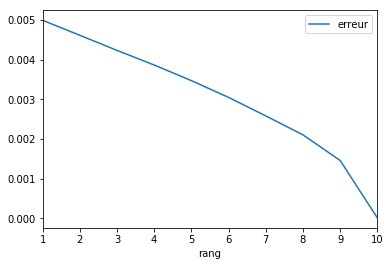
Et maintenant sur une grande et plus nécessairement carrée :

M = rand(300, 10)
mf = NMF(1)
mf.fit_transform(M)
mf.reconstruction_err_ / (M.shape[0] * M.shape[1])

0.004996164872801101

L’erreur est la même :

errs = []
rangs = list(range(1, 11))
for k in rangs:
    mf = NMF(k)
    mf.fit_transform(M)
    e = mf.reconstruction_err_ / (M.shape[0] * M.shape[1])
    errs.append(e)

import pandas
df = pandas.DataFrame(dict(rang=rangs, erreur=errs))
df.plot(x="rang", y="erreur")

<matplotlib.axes._subplots.AxesSubplot at 0x199924d8668>
../_images/valeurs_manquantes_mf_16_1.png

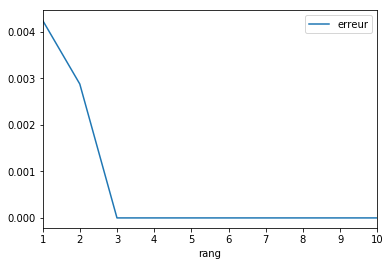
Matrice avec des vecteurs colonnes corrélés#

Supposons maintenant que la matrice précédente M est de rang 3. Pour s’en assurer, on tire une matrice aléalatoire avec 3 vecteurs colonnes et on réplique des colonnes jusqu’à la dimension souhaitée.

from numpy import hstack
M = rand(300, 3)
M = hstack([M, M, M, M[:,:1]])
M.shape

(300, 10)

errs = []
rangs = list(range(1, 11))
for k in rangs:
    mf = NMF(k)
    mf.fit_transform(M)
    e = mf.reconstruction_err_ / (M.shape[0] * M.shape[1])
    errs.append(e)

import pandas
df = pandas.DataFrame(dict(rang=rangs, erreur=errs))
df.plot(x="rang", y="erreur")

<matplotlib.axes._subplots.AxesSubplot at 0x199925d6630>
../_images/valeurs_manquantes_mf_20_1.png

On essaye à nouveausur une matrice un peu plus petite.

M = rand(3, 2)
M = hstack([M, M[:,:1]])
M

array([[ 0.27190312,  0.6497563 ,  0.27190312],
       [ 0.44853292,  0.87097224,  0.44853292],
       [ 0.29424835,  0.65106952,  0.29424835]])

mf = NMF(2)
mf.fit_transform(M)

array([[ 0.61835197,  0.        ],
       [ 0.82887888,  0.29866219],
       [ 0.61960446,  0.07743224]])

mf.components_

array([[ 0.43972536,  1.05078419,  0.43972536],
       [ 0.28143493,  0.        ,  0.28143493]])

La dernière colonne est identique à la première.

Matrice identité#

Et maintenant si la matrice M est la matrice identité, que se passe-t-il ?

from numpy import identity
M = identity(3)
M

array([[ 1.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0.,  1.]])

mf = NMF(1)
mf.fit_transform(M)

array([[ 0.],
       [ 1.],
       [ 0.]])

mf.components_

array([[ 0.,  1.,  0.]])

mf.reconstruction_err_ ** 2

2.0000000000000004

On essaye avec k=2.

mf = NMF(2)
mf.fit_transform(M)

array([[ 0.        ,  0.        ],
       [ 0.        ,  1.03940448],
       [ 0.95521772,  0.        ]])

mf.components_

array([[ 0.        ,  0.        ,  1.04688175],
       [ 0.        ,  0.96208937,  0.        ]])

mf.reconstruction_err_ ** 2

1.0

Avec des vecteurs normés et indépendants (formant donc une base de l’espace vectoriel), l’algorithme aboutit à une matrice W égale au k premiers vecteurs et oublie les autres.

Matrice identité et représentation spatiale#

Pour comprendre un peu mieux ce dernier exemple, il est utile de chercher d’autres solutions dont l’erreur est équivalente.

def erreur_mf(M, W, H):
    d = M - W @ H
    a = d.ravel()
    e = a @ a.T
    e ** 0.5 / (M.shape[0] * M.shape[1])
    return e

M = identity(3)
mf = NMF(2)
W = mf.fit_transform(M)
H = mf.components_
erreur_mf(M, W, H)

1.0

W

array([[ 0.        ,  0.        ],
       [ 0.9703523 ,  0.        ],
       [ 0.        ,  1.02721047]])

H

array([[ 0.        ,  1.03055354,  0.        ],
       [ 0.        ,  0.        ,  0.97351032]])

W @ H

array([[ 0.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0.,  1.]])

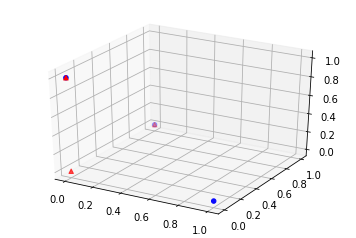
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
wh = W @ H
ax.scatter(M[:,0], M[:,1], M[:,2], c='b', marker='o', s=20)
ax.scatter(wh[:,0], wh[:,1], wh[:,2], c='r', marker='^')

<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x19992d2a5c0>
../_images/valeurs_manquantes_mf_41_1.png

Et si on pose maintenant :

import numpy
W = numpy.array([[0.5, 0.5, 0], [0, 0, 1]]).T
H = numpy.array([[1, 1, 0], [0.0, 0.0, 1.0]])
W

array([[ 0.5,  0. ],
       [ 0.5,  0. ],
       [ 0. ,  1. ]])

H

array([[ 1.,  1.,  0.],
       [ 0.,  0.,  1.]])

W @ H

array([[ 0.5,  0.5,  0. ],
       [ 0.5,  0.5,  0. ],
       [ 0. ,  0. ,  1. ]])

erreur_mf(M, W, H)

1.0

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
wh = W @ H
ax.scatter(M[:,0], M[:,1], M[:,2], c='b', marker='o', s=20)
ax.scatter(wh[:,0], wh[:,1], wh[:,2], c='r', marker='^')

<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x19992a2e5f8>
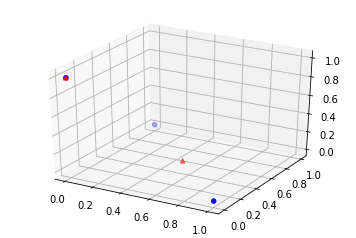
../_images/valeurs_manquantes_mf_47_1.png

On peut voir la matrice M comme un ensemble de n points dans un espace vectoriel. La matrice W est un ensemble de k < n points dans le même espace. La matrice WH, de rang k est une approximation de cet ensemble dans le même espace, c’est aussi n combinaisons linéaires de k points de façon à former n points les plus proches proches de n points de la matrice M.