Note
Click here to download the full example code
Fast design with a python runtime#
ONNX operators do not contain all operators from numpy. There is no operator for solve but this one is needed to implement the prediction function of model NMF. The converter can be written including a new ONNX operator but then it requires a runtime for it to be tested. This example shows how to do that with the python runtime implemented in mlprodict. It may not be onnxruntime but that speeds up the implementation of the converter.
The example changes the transformer from Implement a new converter, the method predict decorrelates the variables by computing the eigen values. Method fit does not do anything anymore.
A transformer which decorrelates variables#
This time, the eigen values are not estimated at training time but at prediction time.
from mlprodict.onnxrt.ops_cpu import OpRunCustom, register_operator
from skl2onnx.algebra.onnx_ops import (
OnnxAdd,
OnnxCast,
OnnxDiv,
OnnxGatherElements,
OnnxEyeLike,
OnnxMatMul,
OnnxMul,
OnnxPow,
OnnxReduceMean,
OnnxShape,
OnnxSub,
OnnxTranspose,
)
from skl2onnx.algebra import OnnxOperator
from mlprodict.onnxrt import OnnxInference
from pyquickhelper.helpgen.graphviz_helper import plot_graphviz
import pickle
from io import BytesIO
import numpy
from numpy.testing import assert_almost_equal
from sklearn.base import TransformerMixin, BaseEstimator
from sklearn.datasets import load_iris
from skl2onnx.common.data_types import guess_numpy_type, guess_proto_type
from skl2onnx import to_onnx
from skl2onnx import update_registered_converter
class LiveDecorrelateTransformer(TransformerMixin, BaseEstimator):
"""
Decorrelates correlated gaussian features.
:param alpha: avoids non inversible matrices
by adding *alpha* identity matrix
*Attributes*
* `self.nf_`: number of expected features
"""
def __init__(self, alpha=0.):
BaseEstimator.__init__(self)
TransformerMixin.__init__(self)
self.alpha = alpha
def fit(self, X, y=None, sample_weights=None):
if sample_weights is not None:
raise NotImplementedError(
"sample_weights != None is not implemented.")
self.nf_ = X.shape[1]
return self
def transform(self, X):
mean_ = numpy.mean(X, axis=0, keepdims=True)
X2 = X - mean_
V = X2.T @ X2 / X2.shape[0]
if self.alpha != 0:
V += numpy.identity(V.shape[0]) * self.alpha
L, P = numpy.linalg.eig(V)
Linv = L ** (-0.5)
diag = numpy.diag(Linv)
root = P @ diag @ P.transpose()
coef_ = root
return (X - mean_) @ coef_
def test_live_decorrelate_transformer():
data = load_iris()
X = data.data
dec = LiveDecorrelateTransformer()
dec.fit(X)
pred = dec.transform(X)
cov = pred.T @ pred
cov /= cov[0, 0]
assert_almost_equal(numpy.identity(4), cov)
dec = LiveDecorrelateTransformer(alpha=1e-10)
dec.fit(X)
pred = dec.transform(X)
cov = pred.T @ pred
cov /= cov[0, 0]
assert_almost_equal(numpy.identity(4), cov)
st = BytesIO()
pickle.dump(dec, st)
dec2 = pickle.load(BytesIO(st.getvalue()))
assert_almost_equal(dec.transform(X), dec2.transform(X))
test_live_decorrelate_transformer()
Everything works as expected.
Extend ONNX#
The conversion requires one operator to compute the eigen values and vectors. The list of ONNX operators does not contain anything which produces eigen values. It does not seem efficient to implement an algorithm with existing ONNX operators to find eigen values. A new operator must be added, we give it the same name Eig as in numpy. It would take a matrix and would produce one or two outputs, the eigen values and the eigen vectors. Just for the exercise, a parameter specifies to output the eigen vectors as a second output.
New ONNX operator#
Any unknown operator can be added to an ONNX graph. Operators are grouped by domain, ‘’ or ai.onnx refers to matrix computation. ai.onnx.ml refers to usual machine learning models. New domains are officially supported by onnx package. We want to create a new operator Eig of domain onnxcustom. It must be declared in a class, then a converter can use it.
class OnnxEig(OnnxOperator):
"""
Defines a custom operator not defined by ONNX
specifications but in onnxruntime.
"""
since_version = 1 # last changed in this version
expected_inputs = [('X', 'T')] # input names and types
expected_outputs = [('EigenValues', 'T'), # output names and types
('EigenVectors', 'T')]
input_range = [1, 1] # only one input is allowed
output_range = [1, 2] # 1 or 2 outputs are produced
is_deprecated = False # obviously not deprecated
domain = 'onnxcustom' # domain, anything is ok
operator_name = 'Eig' # operator name
past_version = {} # empty as it is the first version
def __init__(self, X, eigv=False, op_version=None, **kwargs):
"""
:param X: array or OnnxOperatorMixin
:param eigv: also produces the eigen vectors
:param op_version: opset version
:param kwargs: additional parameters
"""
OnnxOperator.__init__(
self, X, eigv=eigv, op_version=op_version, **kwargs)
print(OnnxEig('X', eigv=True))
OnnxEig(1 in) -> ?
Now we can write the converter and the shape calculator.
shape calculator#
Nothing new here.
def live_decorrelate_transformer_shape_calculator(operator):
op = operator.raw_operator
input_type = operator.inputs[0].type.__class__
input_dim = operator.inputs[0].type.shape[0]
output_type = input_type([input_dim, op.nf_])
operator.outputs[0].type = output_type
converter#
The converter is using the class OnnxEig. The code is longer than previous converters as the computation is more complex too.
def live_decorrelate_transformer_converter(scope, operator, container):
# shortcuts
op = operator.raw_operator
opv = container.target_opset
out = operator.outputs
# We retrieve the unique input.
X = operator.inputs[0]
# We guess its type. If the operator ingests float (or double),
# it outputs float (or double).
proto_dtype = guess_proto_type(X.type)
dtype = guess_numpy_type(X.type)
# Lines in comment specify the numpy computation
# the ONNX code implements.
# mean_ = numpy.mean(X, axis=0, keepdims=True)
mean = OnnxReduceMean(X, axes=[0], keepdims=1, op_version=opv)
# This is trick I often use. The converter automatically
# chooses a name for every output. In big graph,
# it is difficult to know which operator is producing which output.
# This line just tells every node must prefix its ouputs with this string.
# It also applies to all inputs nodes unless this method
# was called for one of these nodes.
mean.set_onnx_name_prefix('mean')
# X2 = X - mean_
X2 = OnnxSub(X, mean, op_version=opv)
# V = X2.T @ X2 / X2.shape[0]
N = OnnxGatherElements(
OnnxShape(X, op_version=opv),
numpy.array([0], dtype=numpy.int64),
op_version=opv)
Nf = OnnxCast(N, to=proto_dtype, op_version=opv)
# Every output involved in N and Nf is prefixed by 'N'.
Nf.set_onnx_name_prefix('N')
V = OnnxDiv(
OnnxMatMul(OnnxTranspose(X2, op_version=opv),
X2, op_version=opv),
Nf, op_version=opv)
V.set_onnx_name_prefix('V1')
# V += numpy.identity(V.shape[0]) * self.alpha
V = OnnxAdd(V,
op.alpha * numpy.identity(op.nf_, dtype=dtype),
op_version=opv)
V.set_onnx_name_prefix('V2')
# L, P = numpy.linalg.eig(V)
LP = OnnxEig(V, eigv=True, op_version=opv)
LP.set_onnx_name_prefix('LP')
# Linv = L ** (-0.5)
# Notation LP[0] means OnnxPow is taking the first output
# of operator OnnxEig, LP[1] would mean the second one
# LP is not allowed as it is ambiguous
Linv = OnnxPow(LP[0], numpy.array([-0.5], dtype=dtype),
op_version=opv)
Linv.set_onnx_name_prefix('Linv')
# diag = numpy.diag(Linv)
diag = OnnxMul(
OnnxEyeLike(
numpy.zeros((op.nf_, op.nf_), dtype=numpy.int64),
k=0, op_version=opv),
Linv, op_version=opv)
diag.set_onnx_name_prefix('diag')
# root = P @ diag @ P.transpose()
trv = OnnxTranspose(LP[1], op_version=opv)
coef_left = OnnxMatMul(LP[1], diag, op_version=opv)
coef_left.set_onnx_name_prefix('coef_left')
coef = OnnxMatMul(coef_left, trv, op_version=opv)
coef.set_onnx_name_prefix('coef')
# Same part as before.
Y = OnnxMatMul(X2, coef, op_version=opv, output_names=out[:1])
Y.set_onnx_name_prefix('Y')
# The last line specifies the final output.
# Every node involved in the computation is added to the ONNX
# graph at this stage.
Y.add_to(scope, container)
Runtime for Eig#
Here comes the new part. The python runtime does not implement any runtime for Eig. We need to tell the runtime to compute eigen values and vectors every time operator Eig is called. That means implementing two methods, one to compute, one to infer the shape of the results. The first one is mandatory, the second one can return an empty shape if it depends on the inputs. If it is known, the runtime may be able to optimize the computation, by reducing allocation for example.
class OpEig(OpRunCustom):
op_name = 'Eig' # operator name
atts = {'eigv': True} # operator parameters
def __init__(self, onnx_node, desc=None, **options):
# constructor, every parameter is added a member
OpRunCustom.__init__(self, onnx_node, desc=desc,
expected_attributes=OpEig.atts,
**options)
def run(self, x, attributes=None, verbose=0, fLOG=print):
# computation
if self.eigv:
return numpy.linalg.eig(x)
return (numpy.linalg.eigvals(x), )
Registration#
update_registered_converter(
LiveDecorrelateTransformer, "SklearnLiveDecorrelateTransformer",
live_decorrelate_transformer_shape_calculator,
live_decorrelate_transformer_converter)
Final example#
data = load_iris()
X = data.data
dec = LiveDecorrelateTransformer()
dec.fit(X)
onx = to_onnx(dec, X.astype(numpy.float32), target_opset=17)
register_operator(OpEig, name='Eig', overwrite=False)
oinf = OnnxInference(onx)
exp = dec.transform(X.astype(numpy.float32))
got = oinf.run({'X': X.astype(numpy.float32)})['variable']
def diff(p1, p2):
p1 = p1.ravel()
p2 = p2.ravel()
d = numpy.abs(p2 - p1)
return d.max(), (d / numpy.abs(p1)).max()
print(diff(exp, got))
(0.0, 0.0)
It works!
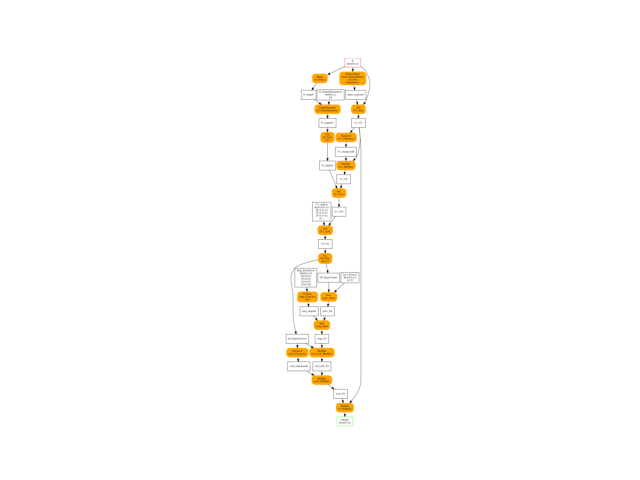
Final graph#
oinf = OnnxInference(onx)
ax = plot_graphviz(oinf.to_dot())
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
Total running time of the script: ( 0 minutes 0.718 seconds)