Note
Go to the end to download the full example code
Classification Binaire#
Un problème de classification binaire consiste à trouver un moyen de séparer deux nuages de points (voir classification).
Principe#
On commence par générer un nuage de points artificiel.
from sklearn.metrics import log_loss
from sklearn.metrics import auc
from sklearn.metrics import roc_curve
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
import numpy
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
X, Y = make_classification(n_samples=500, n_features=2, n_classes=2,
n_repeated=0, n_redundant=0)
On représente ces données.
fig = plt.figure(figsize=(5, 5))
ax = plt.subplot()
ax.plot(X[Y == 0, 0], X[Y == 0, 1], "ob")
ax.plot(X[Y == 1, 0], X[Y == 1, 1], "or")
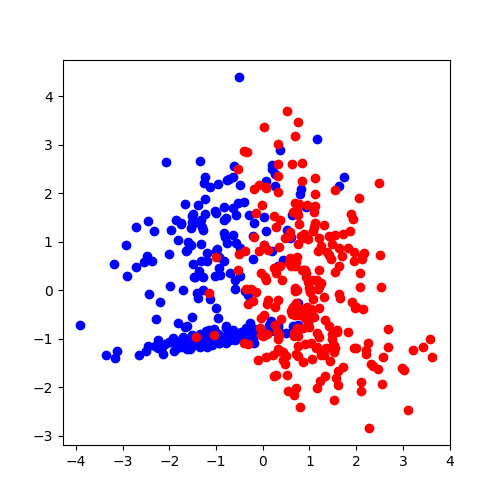
[<matplotlib.lines.Line2D object at 0x7f5f34456e80>]
D’un point de vue géométrique, un problème de classification consiste à trouver la meilleure frontière entre deux nuages de points. Le plus simple est de supposer que c’est une droite. Dans ce cas, on choisira un modèle de régression logistique : LogisticRegression.
logreg = LogisticRegression()
logreg.fit(X, Y)
L’optimisation du modèle produit une droite dont les coefficients sont :
print(logreg.coef_, logreg.intercept_)
[[ 2.44207867 -0.05064282]] [-0.07998426]
Nous pourrions tracer cette droite mais ce graphe ne serait valable que pour un modèle linéaire. Il est aussi facile de colorier le fond du graphe avec la couleur de la classe prédite par le modèle.
def colorie(X, model, ax, fig):
xmin, xmax = numpy.min(X[:, 0]), numpy.max(X[:, 0])
ymin, ymax = numpy.min(X[:, 1]), numpy.max(X[:, 1])
hx = (xmax - xmin) / 100
hy = (ymax - ymin) / 100
xx, yy = numpy.mgrid[xmin:xmax:hx, ymin:ymax:hy]
grid = numpy.c_[xx.ravel(), yy.ravel()]
probs = model.predict_proba(grid)[:, 1].reshape(xx.shape)
contour = ax.contourf(xx, yy, probs, 25, cmap="RdBu", vmin=0, vmax=1)
ax_c = fig.colorbar(contour)
ax_c.set_label("$P(y = 1)$")
ax_c.set_ticks([0, .25, .5, .75, 1])
ax.set_xlim([xmin, xmax])
ax.set_ylim([ymin, ymax])
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot()
colorie(X, logreg, ax, fig)
ax.scatter(X[:, 0], X[:, 1], c=Y, s=50,
cmap="RdBu", vmin=-.2, vmax=1.2,
edgecolor="white", linewidth=1)
ax.set(aspect="equal", xlabel="$X_1$", ylabel="$X_2$")
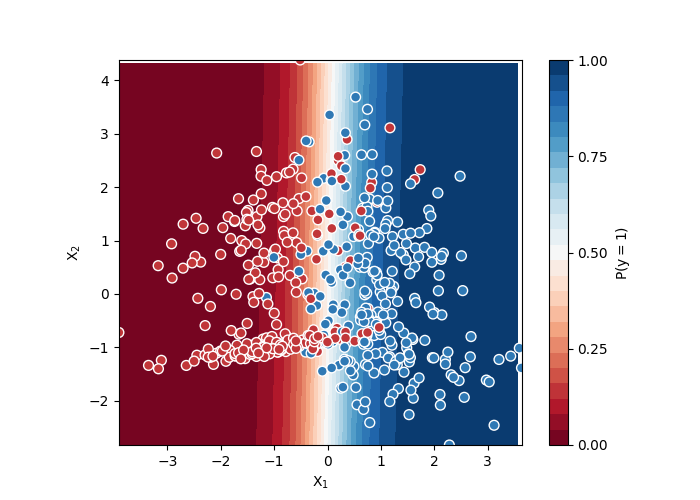
[None, Text(0.5, 25.722222222222214, '$X_1$'), Text(83.10591224957602, 0.5, '$X_2$')]
Evaluation#
Il y a deux tests qu’on effectue de façon quasi-systématique pour ce type de problème : une matrice de confusion et une courbe ROC.
La première étape consiste à diviser les données en base d’apprentissage (train) et base de test (test). C’est nécessaire car certains modèles peuvent simplement apprendre par coeur et l’erreur est sur les données ayant servi à apprendre. C’est le cas des plus proches voisins. La division doit être aléatoire. On peut d’ailleurs recommencer plusieurs pour s’assurer de la robustesse des résultats.
X_train, X_test, y_train, y_test = train_test_split(X, Y)
On apprend sur la base d’apprentissage.
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
Et on prédit sur la base de test.
y_pred = logreg.predict(X_test)
Puis on calcule la matrice de confusion.
conf = confusion_matrix(y_test, y_pred)
print(conf)
[[55 6]
[11 53]]
Les nombres sur la diagonale indiquent les éléments classés dans la bonne classe. Ailleurs, il s’agit des éléments mal classés par le modèle. Ce sont des points bleus sur un fond rouge par exemple.
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot()
colorie(X_test, logreg, ax, fig)
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, s=50,
cmap="RdBu", vmin=-.2, vmax=1.2,
edgecolor="white", linewidth=1)
ax.set(aspect="equal", xlabel="$X_1$", ylabel="$X_2$")
ax.set_title("Résultats sur la base de test")
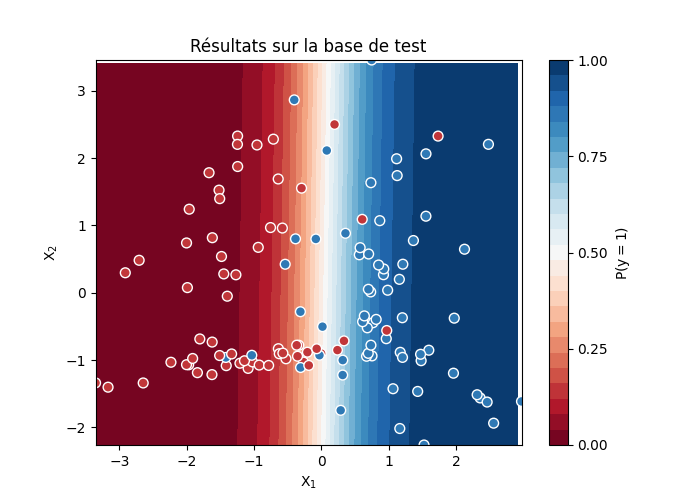
Text(0.5, 1.0, 'Résultats sur la base de test')
Certains points sont plus ou moins éloignés de la frontière que le modèle a trouvé entre les deux classes. Plus le point est loin de la frontière, plus le modèle est sûr de lui. C’est vrai pour la régression logistique mais aussi pour la plupart des modèles utilisés pour faire une classification binaire. C’est comme cela que le modèle est capable de donner un indicateur de confiance : la distance du point à la frontière que le modèle a trouvé. Cette distance est convertie en score ou en probabilité. La matrice de confusion n’utilise pas cette information, la courbe ROC si. Voyons comment. On s’inspire de l’exemple Receiver Operating Characteristic (ROC). La courbe ROC ne change pas qu’on choisisse un score ou une probabilité. On calcule les probabilités. Le modèle retourne la probabilité que chaque exemple appartienne dans chacune des classes.
y_proba = logreg.predict_proba(X_test)
print(y_proba[:3])
[[0.14774986 0.85225014]
[0.10717777 0.89282223]
[0.9821646 0.0178354 ]]
On construit la courbe ROC.
Tout d’abord les coordonnées des points.
Le modèle prédit bien si le modèle trouve la bonne classe
ce qu’on traduit par y_pred == y_test.
Le score est celui de la classe prédite :
y_score[y_pred].
prob_pred = [y_proba[i, c] for i, c in enumerate(y_pred)]
fpr, tpr, th = roc_curve((y_pred == y_test).ravel(), prob_pred)
Pour un indice i, th[i] est un seuil,
tpr[i] est la proportion d’exemples bien classés pour lesquels
le score du modèle est supérieur th[i].
fpr[i] est la proportion d’exemples mal classés pour lesquels
le score du modèle est supérieur th[i].
print("i=2", th[2], tpr[2], fpr[2])
print(f"i={len(th) - 2}", th[-2], tpr[-2], fpr[-2])
i=2 0.984833882844044 0.25 0.0
i=24 0.5360625604318461 1.0 0.8823529411764706
Plus le score est faible, plus ces proportions sont grandes. Quand le seuil est très faible, le modèle retourne un score toujours supérieur au seuil. Les deux proportions sont égales à 1. A l’inverse, si le seuil est élevé, les deux proportions sont nulles. On trace la courbe en faisant varier le seuil.
plt.figure()
lw = 2
plt.plot(fpr, tpr, color='darkorange', lw=lw, label='Courbe ROC')
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel("Proportion mal classée")
plt.ylabel("Proportion bien classée")
plt.title('ROC')
plt.legend(loc="lower right")
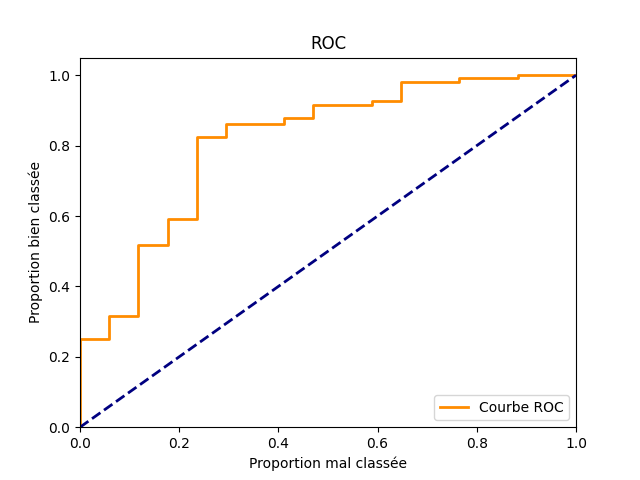
<matplotlib.legend.Legend object at 0x7f5f3432b490>
L’aire sous la courbe ou AUC (Area Under the Curve) est liée à la pertinence du modèle. Plus le score est elevé, plus on s’attend à ce que la proportion d’exemples bien classés soit grande par rapport à la proportion d’exemple mal classés. A l’inverse, quand ces proportions sont toujours égales quelque soit le sueil, la courbe correspond à la première diagonale et le modèle n’a rien appris. Plus la courbe est haute, meilleur le modèle est. C’est pourquoi on calcule l’aire sous la courbe.
print(auc(fpr, tpr))
0.8120915032679739
La courbe ROC s’applique toujours à un problème de classification binaire qu’on peut scinder en trois questions :
Le modèle a bien classé un exemple dans la classe 0.
Le modèle a bien classé un exemple dans la classe 1.
Le modèle a bien classé un exemple, que ce soit dans la classe 0 ou la classe 1. Ce problème suppose implicitement
- que le même seuil est utilisé sur chacun des classes.
C’est-à-dire qu’on prédit la classe 1 si le score pour la classe 1 est supérieur à à celui obtenu pour la classe 0 mais aussi qu’on valide la réponse si le score de la classe 1 ou celui de la classe 0 est supérieur au même seuil s, ce qui n’est pas nécessairement le meilleur choix.
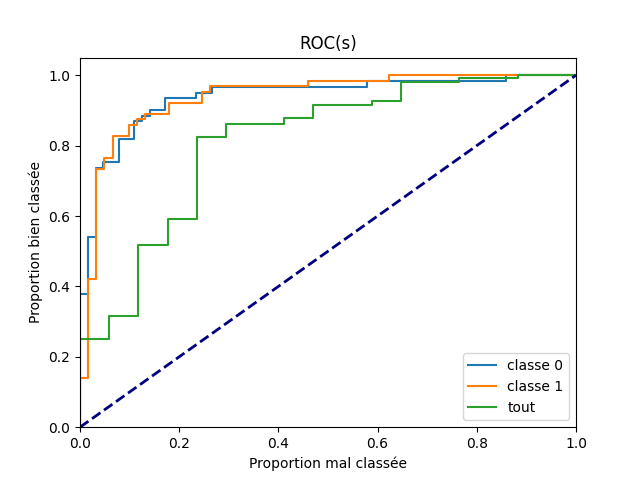
Si les réponses sont liées, le modèle peut répondre de manière plus ou moins efficace à ces trois questions. On calcule les courbes ROC à ces trois questions.
fpr_cl = dict()
tpr_cl = dict()
fpr_cl["classe 0"], tpr_cl["classe 0"], _ = roc_curve(
y_test == 0, y_proba[:, 0].ravel())
fpr_cl["classe 1"], tpr_cl["classe 1"], _ = roc_curve(
y_test, y_proba[:, 1].ravel()) # y_test == 1
fpr_cl["tout"], tpr_cl["tout"] = fpr, tpr # On reprend ceux déjà calculés.
Et on les représente.
plt.figure()
for key in fpr_cl:
plt.plot(fpr_cl[key], tpr_cl[key], label=key)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel("Proportion mal classée")
plt.ylabel("Proportion bien classée")
plt.title('ROC(s)')
plt.legend(loc="lower right")
<matplotlib.legend.Legend object at 0x7f5f34250160>
Fonctions de coût#
La performance d’un modèle est parfois évaluée avec une fonction de coût
qui n’est pas celle utilisée pour optimiser le modèle. C’est le cas
souvent de l’aire sous la courbe d’une courbe ROC (AUC). Dans la plupart
des cas, le modèle n’est pas optimisée pour cette métrique.
La métrique AUC est coûteuse à calculer, c’est pourquoi on lui
préfère souvent d’autres métriques comme :
la logloss.
Si on note la classe attendue et
la probabilité
que l’observation i appartiennent à cette classe selon le modèle, alors :
On utilise la fonction :epkg:`scikit-learn:metrics:log_loss`.
err = log_loss(y_test, y_proba)
print(err)
0.32113050602407
Total running time of the script: ( 0 minutes 2.897 seconds)