Note

Go to the end to download the full example code

Réduction des dimensions#

On peut souhaiter réduire de nombre de dimensions d’un jeu de données :

pour le compresser : diminution le volume d’informations utiles à stocker et par la même occasion la durée d’exécution d’un algorithme d’apprentisssage (car l’espace à explorer est plus petit).
pour réduire le bruit et éviter ainsi le surapprentissage (apprentissage du bruit dans les données).

Préparation - Import #

import matplotlib.pyplot as plt  # traçage de graphiques
import numpy as np  # traitement des arrays numériques
import pandas as pd

from sklearn import datasets  # datasets classiques
from sklearn import preprocessing  # normalisation les données
from sklearn import decomposition  # PCA et NMF
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis  # LDA

np.random.seed = 2017  # pour des résultats reproductibles

PCA - L’analyse en composante principale #

L’analyse en composante principale pour des données numériques en n dimensions est un algorithme non supervisé d’identification des dimensions de variance décroissante et de changement de base pour ne conserver que les k dimensions de plus grande variance.

Il consiste à :

Optionnel : Normaliser les données (important si les données n’ont par exemple pas été mesurées aux mêmes échelles).
Construire la matrice de covariance entre les variables : $\Sigma = \frac{1}{n-1}\sum_{i=1}^{n}{((X - \bar{x})'(X - \bar{x}))}$ .
Trouver les valeurs propres $\lambda_i$ et vecteurs propres $v_i$ : $\Sigma v_i = \lambda_iv_i$ , ces vecteurs propres forment un repère orthogonal de l’espace des données (en tant que vecteurs propres d’une matrice symmétrique qu’on supposera de rang n).
Classer les valeurs propres (et les vecteurs associés) de façon décroissante : $\{\lambda_{(n)}, \lambda_{(n-1)}...\lambda_{(1)} \}$ où $\lambda_{(i)}$ est la i-ème variance dans l’ordre croissant.
Ne conserver que les k ( $k \leqslant n$ ) premiers vecteurs : $\{v_{(n)}, v_{(n-1)}...v_{(n-k+1)} \}$ .
Construire la matrice de projection dans l’espace de ces vecteurs (changement de base si n=k).
Projeter les données initiales dans cet espace de dimension k.

Tout cela peut bien sur être implémenté from scratch avec Numpy mais nous utiliserons ici scikit-learn pour raccourcir l’implémentation et nous concentrer sur la visualisation des résultats. Cf. Analyse en composantes principales (ACP) et PCA.

Implémentation avec scikit-learn #

Données

Nous partirons classiquement du dataset Iris (classification de 3 fleurs sur la base de certaines de leurs mesures) :

iris = datasets.load_iris()
X_iris = iris.data
y_iris = iris.target

print(f"Dimensions de l'espace de départ : {X_iris.shape[1]}")
print("Représentation des données dans ces dimensions :")

plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.title("Dimensions 0 et 1:")
plt.scatter(X_iris[:, 0], X_iris[:, 1], c=y_iris)
plt.subplot(1, 2, 2)
plt.title("Dimensions 2 et 3:")
plt.scatter(X_iris[:, 2], X_iris[:, 3], c=y_iris)
plt.plot([1, 7], [0.05, 2.5])

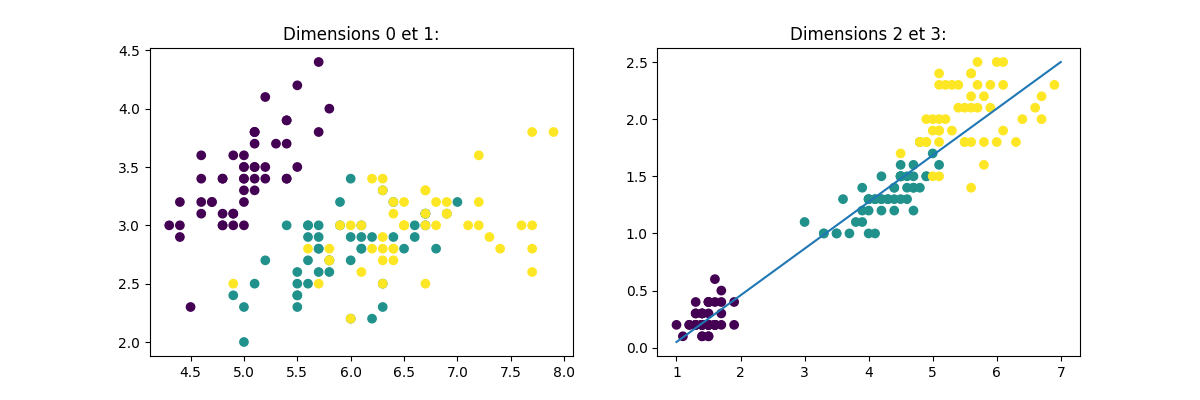
Dimensions de l'espace de départ : 4
Représentation des données dans ces dimensions :

[<matplotlib.lines.Line2D object at 0x7f5f36919b20>]

Premier exemple de PCA

Graphiquement, on peut se dire que les 2 dernières dimensions sont très corrélées et donc redondantes. Dans un strict but de classification, on pourrait d’ailleurs presque se contenter de la dimension indiquée par la ligne bleue pour correctement discriminer les 3 types de fleurs (nous verrons par la suite qu’il s’agit d’un cas particulier non généralisable).

Effectuons une PCA avec scikit-learn avec un changemment de base conservant les 4 dimensions pour illustrer leurs différences : Gardons toutes les composantes pour le moment, nous pourrons toujours en retirer ensuite puisqu’elles seront triées par significativité

pca = decomposition.PCA(n_components=4)
X_iris_PCA = pca.fit(X_iris).transform(X_iris)

On dessine.

def graph_acp2(X_PC2, y):
    plt.figure(figsize=(15, 4))
    plt.subplot(1, 3, 1)
    plt.xlabel('Principal Component 1')
    plt.ylabel('Principal Component 2')
    plt.scatter(X_PC2[:, 0], X_PC2[:, 1], c=y)
    plt.subplot(1, 3, 2)
    plt.title("Dimension de la plus grande variance :")
    plt.scatter(X_PC2[:, 0], np.ones(X_PC2.shape[0]), c=y)
    plt.subplot(1, 3, 3)
    plt.title("Dimension de 2nde variance :")
    plt.scatter(X_PC2[:, 1], np.ones(X_PC2.shape[0]), c=y)


graph_acp2(X_iris_PCA, y_iris)

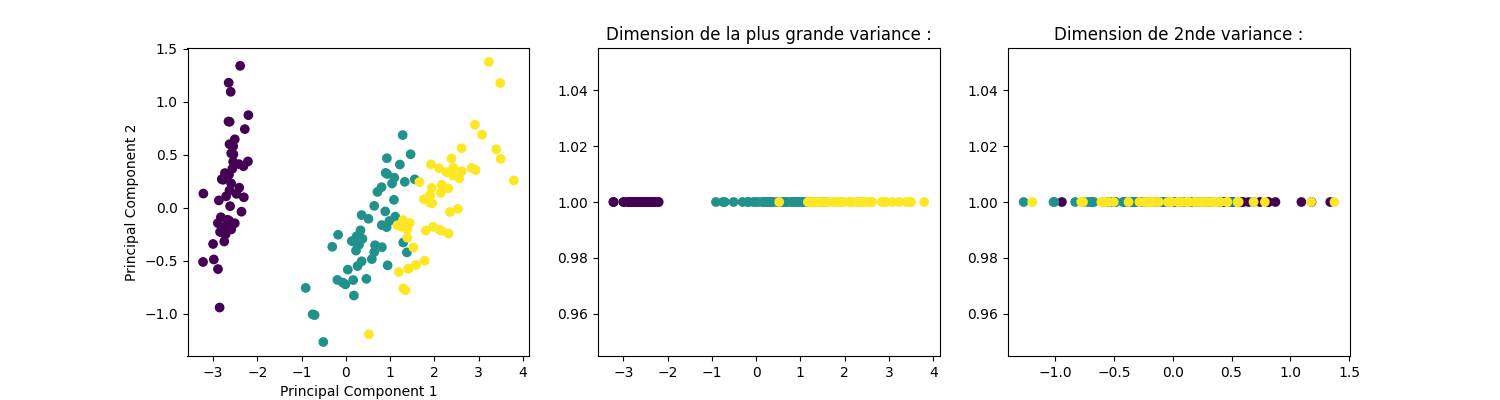
Dimension de la plus grande variance :, Dimension de 2nde variance :

Quelques réserves

Comme évoqué dans la présentation, il est à noter qu’il s’agit d’un algorithme non supervisé, qui ne tient donc pas compte des étiquettes des données. Dans le cas ci-dessus, nous avons eu la chance que les données soient linéairement séparables sur la dimension de plus grande variance. Dans le cas contraire, l’ACP aurait pu ne pas nous aider et nous aurions même pu perdre les dimensions selon lesquelles discriminer les données correctement.

A noter également que dans le cas de données de variance assez homogène selon toutes les dimensions, une ACP ne nous apporte rien.

L’ACP peut donc être inutile voire contreproductive dans un objectif de classification.

Ci-après 2 contre-exemples :

ACP et discrimination selon dimension de moindre variance

X11 = np.random.rand(30) * 10
X21 = X11 + 1
X12 = np.random.rand(20) * 10
X22 = X12 + 2
X = np.array([np.concatenate((X11, X12)),
              np.concatenate((X21, X22))]).T
y = np.concatenate((np.zeros(30), np.ones(20)))
X = preprocessing.scale(X, with_mean=True, with_std=True)

plt.scatter(X[:, 0], X[:, 1], c=y)

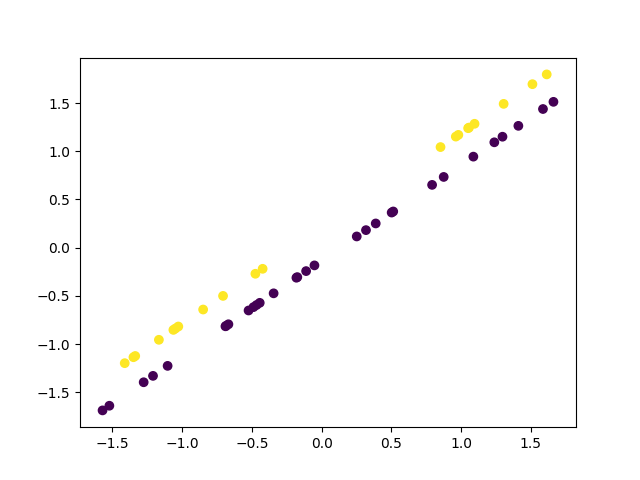
<matplotlib.collections.PathCollection object at 0x7f5f35e6b1f0>

Et l’ACP :

pca = decomposition.PCA(n_components=2)
X_PC2 = pca.fit(X).transform(X)
graph_acp2(X_PC2, y)

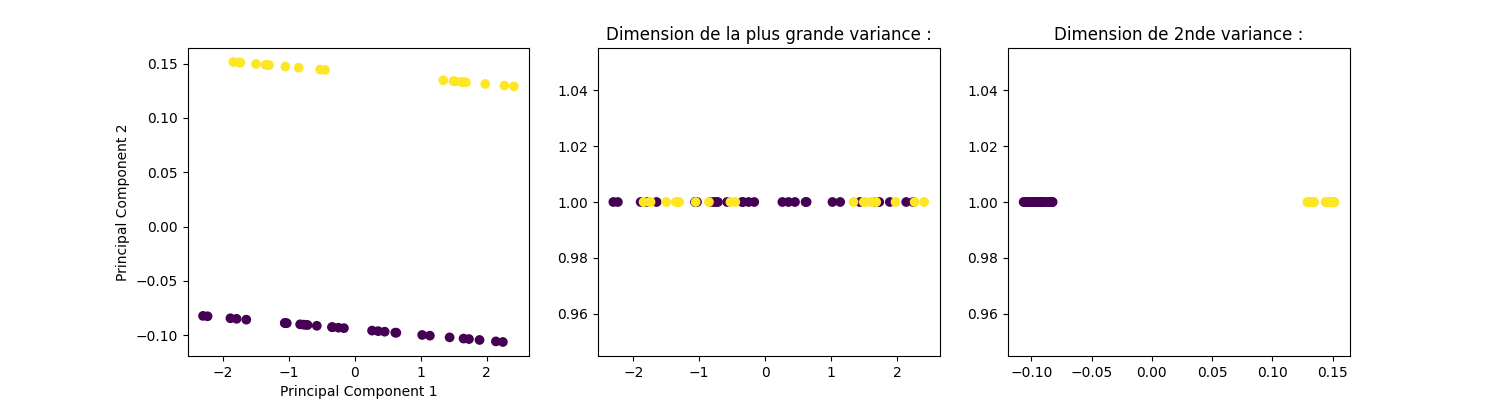
Ici une ACP ne retenant que la dimension de plus grande variance nous aurait donc fait perdre toute possibilité de discrimination.

ACP sur des données de variance homogène #

X11 = np.random.normal(0, 10, 500)
X21 = abs(np.random.normal(0, 10, 500))
X12 = np.random.normal(0, 10, 500)
X22 = -abs(np.random.normal(0, 10, 500))
X = np.array([np.concatenate((X11, X12)),
              np.concatenate((X21, X22))]).T
y = np.concatenate((np.zeros(500), np.ones(500)))
y = y.astype(int)

plt.figure(figsize=(6, 6))
plt.scatter(X[:, 0], X[:, 1], c=y)

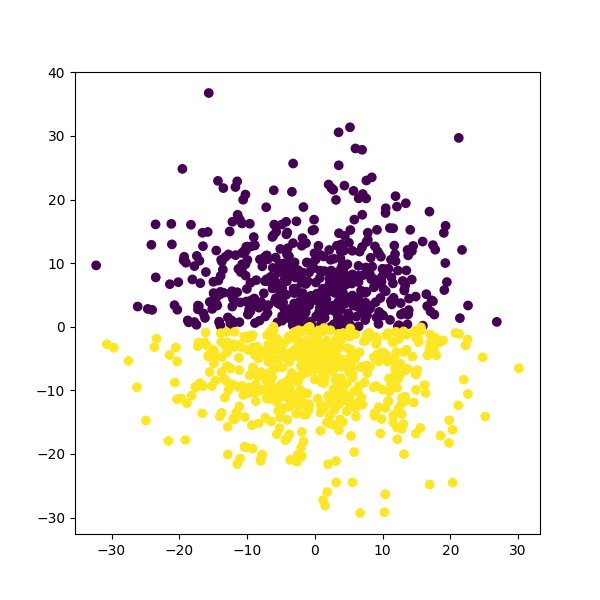
<matplotlib.collections.PathCollection object at 0x7f5f341aa7f0>

Et l’ACP :

pca = decomposition.PCA(n_components=2)
pca.fit(X)
X_PC2 = pca.transform(X)
graph_acp2(X_PC2, y)

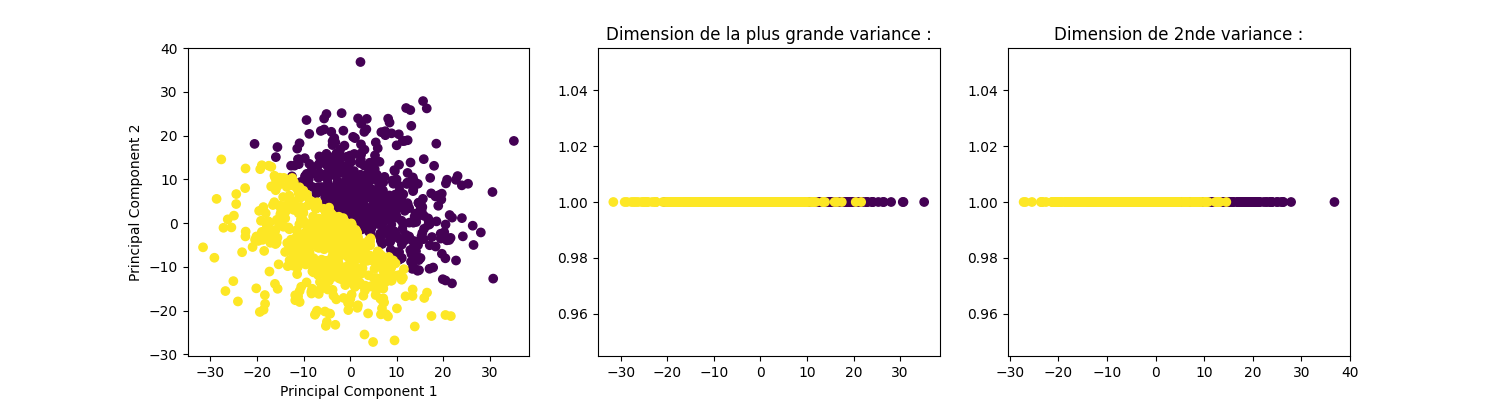
Ici une ACP est inutile car la variance des données est homogène selon les dimensions initiales (cf. orientation diagonale entre les 2 classes). D’autres méthodes, que nous détaillerons moins pour le moment, peuvent être plus pertinentes que l’ACP dans certains contextes :

L’analyse discriminante linéaire ou quadratique (LDA, QDA)#

Voir lda, qda.

Plutôt que de maximiser la variance sur des dimensions des données, on va ici chercher à maximiser la variance inter-classes par rapport à celle intra classe. Cette méthode transformera donc l’espace d’origine en un espace plus adapté que l’ACP dans un objectif de classification.

lda = LinearDiscriminantAnalysis(n_components=2)
X_iris_LDA = lda.fit(X_iris, y_iris).transform(X_iris)

print("Rappel des composantes identifiées par le PCA :")
graph_acp2(X_iris_PCA, y_iris)

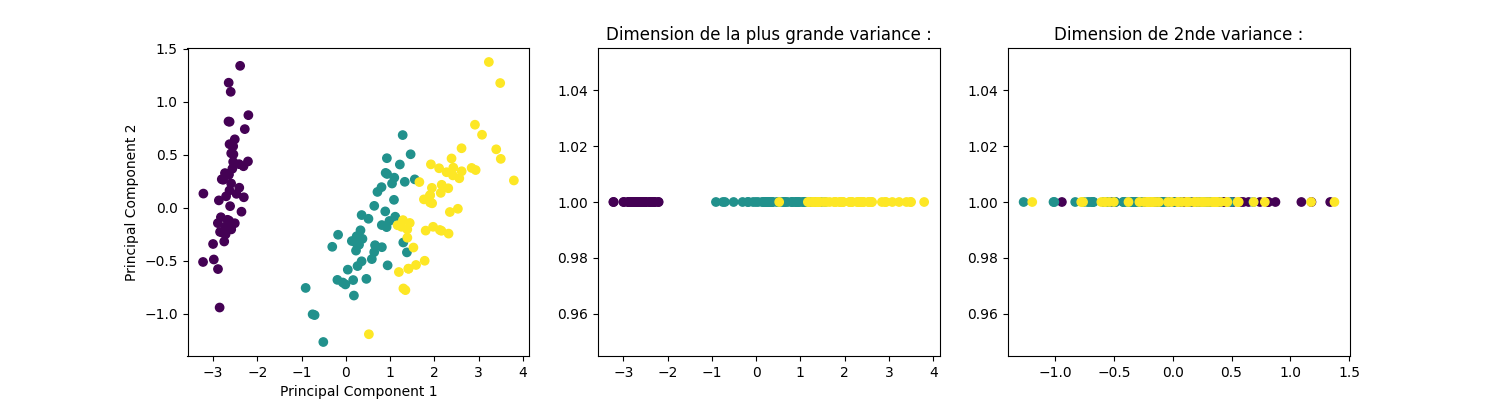
Rappel des composantes identifiées par le PCA :

Composantes.

print("Composantes identifiées par le LDA (on remarque une meilleure "
      "séparation des classes sur la 1ère composante) :")
graph_acp2(X_iris_LDA, y_iris)

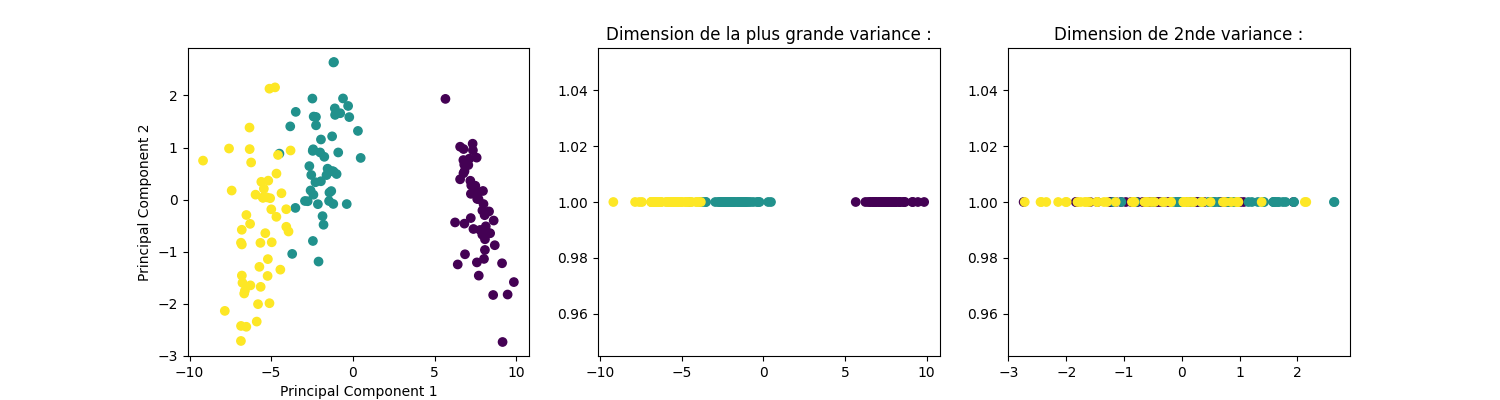
Composantes identifiées par le LDA (on remarque une meilleure séparation des classes sur la 1ère composante) :

Factorisation de matrice #

Voir NMF.

On va ici chercher à approcher une matrice V de dimensions m*n, de grande taille souvent creuse et positive (e.g. les évaluations de tous les clients sur tous les produits dans un site marchand), par un produit d’une matrice W de dimensions m*k (e.g. le profils de tous les clients) avec une matrice H de dimensions k*n (e.g. les évaluations moyennes pour ces profils). Nous chercherons ainsi à avoir $(m*k + k*n) << m*n$ pour diminuer l’espace de représentation de nos données, tout en conservant le maximum d’information.

$\begin{bmatrix} v_{11} & v_{12} & v_{13} & \dots & v_{1n} \\ v_{21} & v_{22} & v_{23} & \dots & v_{2n} \\ v_{31} & V_{32} & v_{33} & \dots & v_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ v_{m1} & V_{m2} & v_{m3} & \dots & v_{mn} \end{bmatrix} = \begin{bmatrix} w_{11} & \dots & w_{1k} \\ w_{21} & \dots & w_{2k} \\ w_{31} & \dots & w_{3k} \\ \vdots & \ddots & \vdots \\ w_{m1} & \dots & w_{mk} \end{bmatrix} * \begin{bmatrix} h_{11} & h_{12} & h_{13} & \dots & h_{1n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ h_{k1} & h_{k2} & h_{k3} & \dots & h_{kn} \end{bmatrix}$

Sans entrer dans les détails, ces algorithmes consisteront à trouver W et H qui minimisent $||V - W*H ||_F^2$ . Il est à noter que la solution minimisant cette norme peut ne pas être unique. De plus ces algorithmes sont multiples, souvent de complexité computationnelle élevée et requièrent des régularisations.

A titre d’exemple construisons une matrice de notations de films par des utilisateurs que nous allons tâcher de factoriser en une matrice de profils (les goûts de chaque utilisateurs) et une autre de catégories de films (les profils auxquels ces films sont susceptibles de plaire). Ces notations vont de 1 à 9 et on désignera par 0 l’absence de note. Cet exemple est volontairement simpliste et ne peut pas passer à l’échelle ni être généralisé trivialement.

df = pd.DataFrame.from_dict({'loves_everything': [9, 9, 9, 9, 9, 9, 0],
                             'big_guns': [1, 2, 1, 8, 9, 8, 9],
                             'testosterone guy': [0, 0, 1, 9, 9, 9, 7],
                             'girlygirl': [9, 0, 8, 1, 0, 0, 7],
                             'romance_addict': [9, 8, 0, 0, 0, 1, 0],
                             'machoman': [0, 1, 0, 8, 7, 9, 8],
                             'loves_flowers': [7, 8, 0, 0, 0, 0, 8],
                             'easily_pleased': [0, 8, 8, 0, 7, 9, 7],
                             'chuck_norris_fan': [0, 2, 0, 9, 0, 9, 8],
                             'mylittleponey98': [7, 0, 7, 0, 1, 0, 8],
                             'allmoviesrock': [7, 8, 0, 0, 7, 8, 7],
                             'more_guns_please': [0, 2, 0, 9, 8, 0, 7],
                             'yeah_guns666': [1, 0, 3, 0, 9, 9, 0]},
                            ).transpose()
df.index.name = "Users"
df.columns = ['Charming prince', 'First date', 'Lovely love',
              'Guns are cool', 'Ultra badass 4', 'My fist in your face',
              'Guns & roses']
df.columns.name = "Movies"
print(df)

Movies            Charming prince  ...  Guns & roses
Users                              ...
loves_everything                9  ...             0
big_guns                        1  ...             9
testosterone guy                0  ...             7
girlygirl                       9  ...             7
romance_addict                  9  ...             0
machoman                        0  ...             8
loves_flowers                   7  ...             8
easily_pleased                  0  ...             7
chuck_norris_fan                0  ...             8
mylittleponey98                 7  ...             8
allmoviesrock                   7  ...             7
more_guns_please                0  ...             7
yeah_guns666                    1  ...             0

[13 rows x 7 columns]

Et la factorisation :

nmf = decomposition.NMF(n_components=2,
                        random_state=1,
                        alpha_W=0.1,
                        alpha_H='same',
                        l1_ratio=.5).fit(df)

profiles = pd.DataFrame(nmf.transform(df),
                        index=df.index,
                        columns=['action lover', 'romcom lover'])
profiles.columns.name = 'Categories'
print(profiles)

Categories        action lover  romcom lover
Users
loves_everything      2.684265      2.229756
big_guns              0.267938      3.043581
testosterone guy      0.000000      3.112098
girlygirl             2.552182      0.052289
romance_addict        2.273587      0.000000
machoman              0.000000      2.912490
loves_flowers         2.458405      0.125417
easily_pleased        1.644423      1.990572
chuck_norris_fan      0.081973      2.325361
mylittleponey98       2.182508      0.214792
allmoviesrock         2.113825      1.649155
more_guns_please      0.051734      2.096170
yeah_guns666          0.076642      1.818309

On filtre :

profiles = profiles > 1
print(profiles)

Categories        action lover  romcom lover
Users
loves_everything          True          True
big_guns                 False          True
testosterone guy         False          True
girlygirl                 True         False
romance_addict            True         False
machoman                 False          True
loves_flowers             True         False
easily_pleased            True          True
chuck_norris_fan         False          True
mylittleponey98           True         False
allmoviesrock             True          True
more_guns_please         False          True
yeah_guns666             False          True

Deux catégories :

movie_cat = pd.DataFrame(nmf.components_,
                         columns=df.columns,
                         index=['action lover', 'romcom lover'])
movie_cat.index.name = 'Categories'
movie_cat = movie_cat > 1

print(movie_cat)

# Nous avons donc bien obtenu une matrice de profils et une autre de
# catégories de films dont la multiplication nous donnera
# approximativement les goûts des utilisateurs pour chaque film, y compris
# ceux qu'ils n'ont pas vus ou évalués.

Movies        Charming prince  First date  ...  My fist in your face  Guns & roses
Categories                                 ...
action lover             True        True  ...                 False          True
romcom lover            False       False  ...                  True          True

[2 rows x 7 columns]

Total running time of the script: ( 0 minutes 7.362 seconds)

Gallery generated by Sphinx-Gallery

Réduction des dimensions#

Préparation - Import#

PCA - L’analyse en composante principale#

Algorithme#

Implémentation avec scikit-learn#

ACP sur des données de variance homogène#