Prédiction, COVID en France, série temporelle#
Links: notebook, html, PDF, python, slides, GitHub
On s’intéresse aux séries temporelles de l’épidémie du COVID en France récupérées depuis data.gouv.fr : Chiffres-clés concernant l’épidémie de COVID19 en France.
from jyquickhelper import add_notebook_menu
add_notebook_menu()
%matplotlib inline
Données#
from pandas import DataFrame, read_csv, to_datetime
df = read_csv("https://www.data.gouv.fr/en/datasets/r/0b66ca39-1623-4d9c-83ad-5434b7f9e2a4")
df['date'] = to_datetime(df['date'].apply(lambda s: s.replace("_", "-")))
df.tail()
c:python387_x64libsite-packagesIPythoncoreinteractiveshell.py:3146: DtypeWarning: Columns (17,18) have mixed types.Specify dtype option on import or set low_memory=False. has_raised = await self.run_ast_nodes(code_ast.body, cell_name,
| date | granularite | maille_code | maille_nom | cas_confirmes | cas_ehpad | cas_confirmes_ehpad | cas_possibles_ehpad | deces | deces_ehpad | reanimation | hospitalises | nouvelles_hospitalisations | nouvelles_reanimations | gueris | depistes | source_nom | source_url | source_archive | source_type | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 43080 | 2021-02-10 | region | REG-75 | Nouvelle-Aquitaine | NaN | NaN | NaN | NaN | 2510.0 | NaN | 213.0 | 1524.0 | 78.0 | 20.0 | 10227.0 | NaN | OpenCOVID19-fr | NaN | NaN | opencovid19-fr |
| 43081 | 2021-02-10 | region | REG-76 | Occitanie | NaN | NaN | NaN | NaN | 2882.0 | NaN | 276.0 | 1886.0 | 121.0 | 25.0 | 12801.0 | NaN | OpenCOVID19-fr | NaN | NaN | opencovid19-fr |
| 43082 | 2021-02-10 | region | REG-84 | Auvergne-Rhône-Alpes | NaN | NaN | NaN | NaN | 8453.0 | NaN | 400.0 | 3699.0 | 213.0 | 42.0 | 34579.0 | NaN | OpenCOVID19-fr | NaN | NaN | opencovid19-fr |
| 43083 | 2021-02-10 | region | REG-93 | Provence-Alpes-Côte d'Azur | NaN | NaN | NaN | NaN | 5010.0 | NaN | 438.0 | 3581.0 | 240.0 | 33.0 | 24080.0 | NaN | OpenCOVID19-fr | NaN | NaN | opencovid19-fr |
| 43084 | 2021-02-10 | region | REG-94 | Corse | NaN | NaN | NaN | NaN | 133.0 | NaN | 7.0 | 58.0 | 4.0 | 3.0 | 587.0 | NaN | OpenCOVID19-fr | NaN | NaN | opencovid19-fr |
from datetime import datetime
gr = df[["date", "cas_confirmes"]].groupby("date").sum().sort_index()
gr.loc[datetime(2020, 11, 11), 'cas_confirmes'] = (
gr.loc[datetime(2020, 11, 10), 'cas_confirmes'] + gr.loc[datetime(2020, 11, 12), 'cas_confirmes']) / 2
gr.loc[gr.index >= datetime(2020, 9, 1), 'cas_confirmes'].plot(figsize=(14, 4), grid=True, title="Cas positifs");
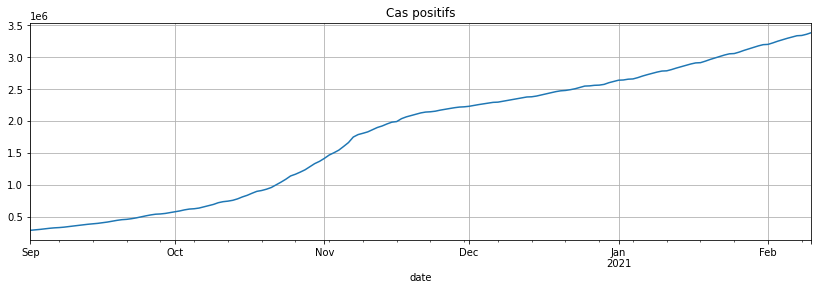
covsept = gr.loc[gr.index >= datetime(2020, 9, 1), 'cas_confirmes']
covsept.diff().plot(figsize=(14, 4), grid=True, title="Cas positifs quotidiens");
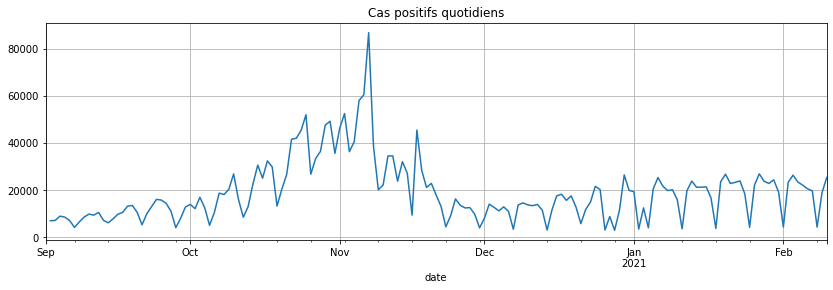
Prédiction : AR#
Autocorrélogramme#
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
data = covsept.diff()[1:]
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = plot_acf(data, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = plot_pacf(data, lags=40, ax=ax2);
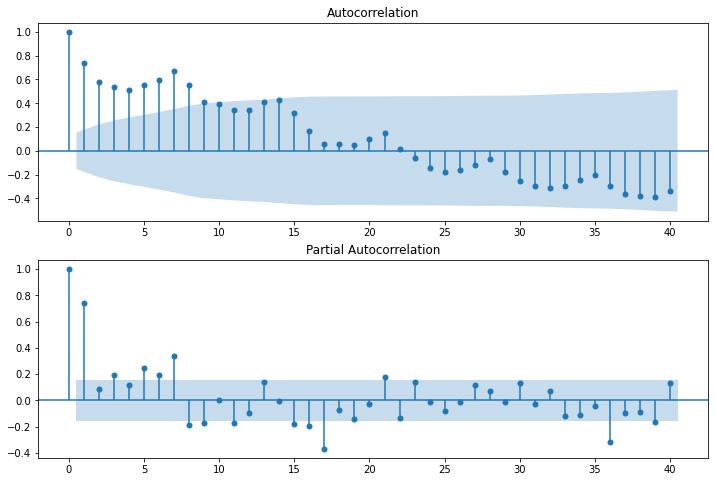
ARIMA#
from statsmodels.tsa.arima.model import ARIMA
mod = ARIMA(data, order=(7, 1, 1))
res = mod.fit()
print(res.summary())
c:python387_x64libsite-packagesstatsmodelstsabasetsa_model.py:524: ValueWarning: No frequency information was provided, so inferred frequency D will be used.
warnings.warn('No frequency information was'
c:python387_x64libsite-packagesstatsmodelstsabasetsa_model.py:524: ValueWarning: No frequency information was provided, so inferred frequency D will be used.
warnings.warn('No frequency information was'
c:python387_x64libsite-packagesstatsmodelstsabasetsa_model.py:524: ValueWarning: No frequency information was provided, so inferred frequency D will be used.
warnings.warn('No frequency information was'
SARIMAX Results
==============================================================================
Dep. Variable: cas_confirmes No. Observations: 162
Model: ARIMA(7, 1, 1) Log Likelihood -1665.458
Date: Thu, 11 Feb 2021 AIC 3348.917
Time: 00:17:40 BIC 3376.649
Sample: 09-02-2020 HQIC 3360.177
- 02-10-2021
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.2273 0.162 1.407 0.159 -0.089 0.544
ar.L2 -0.1927 0.077 -2.508 0.012 -0.343 -0.042
ar.L3 -0.0039 0.103 -0.038 0.970 -0.206 0.199
ar.L4 -0.1243 0.102 -1.216 0.224 -0.324 0.076
ar.L5 0.0696 0.078 0.895 0.371 -0.083 0.222
ar.L6 -0.0285 0.076 -0.374 0.708 -0.177 0.121
ar.L7 0.3801 0.056 6.750 0.000 0.270 0.491
ma.L1 -0.6858 0.167 -4.098 0.000 -1.014 -0.358
sigma2 5.996e+07 1.57e-09 3.81e+16 0.000 6e+07 6e+07
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 289.45
Prob(Q): 1.00 Prob(JB): 0.00
Heteroskedasticity (H): 1.46 Skew: 0.31
Prob(H) (two-sided): 0.17 Kurtosis: 9.54
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[2] Covariance matrix is singular or near-singular, with condition number 3.36e+32. Standard errors may be unstable.
import numpy
pred = DataFrame({"cas+":data.copy()})
pred['pred'] = numpy.nan
pred['pred'] = res.forecasts.ravel()
pred.tail()
| cas+ | pred | |
|---|---|---|
| date | ||
| 2021-02-06 | 20586.0 | 20346.037004 |
| 2021-02-07 | 19715.0 | 19741.530365 |
| 2021-02-08 | 4317.0 | 14212.567962 |
| 2021-02-09 | 18870.0 | 14869.262634 |
| 2021-02-10 | 25387.0 | 23740.270465 |
res.forecasts.ravel()[-5:]
array([20346.03700422, 19741.53036487, 14212.56796166, 14869.2626336 ,
23740.27046459])
res.forecast(7)
2021-02-11 21924.732356
2021-02-12 21223.595082
2021-02-13 18260.072157
2021-02-14 18045.532220
2021-02-15 13187.175698
2021-02-16 17328.572392
2021-02-17 22102.419937
Freq: D, Name: predicted_mean, dtype: float64
pred.plot();
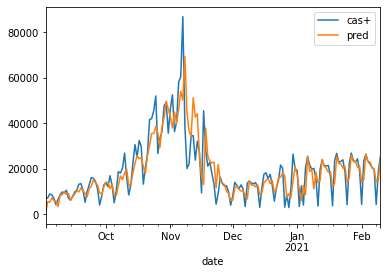
Approche machine learning#
def lagged_dataframe(data, lag=7):
res = data.copy()
data = res.iloc[:, 0]
for i in range(1, lag):
res['l%i' % i] = data.shift(i)
return res[lag:].copy()
lagged_dataframe(DataFrame({'cas+': data}), 8)
| cas+ | l1 | l2 | l3 | l4 | l5 | l6 | l7 | |
|---|---|---|---|---|---|---|---|---|
| date | ||||||||
| 2020-09-10 | 9843.0 | 8577.0 | 6544.0 | 4203.0 | 7071.0 | 8550.0 | 8975.0 | 7157.0 |
| 2020-09-11 | 9406.0 | 9843.0 | 8577.0 | 6544.0 | 4203.0 | 7071.0 | 8550.0 | 8975.0 |
| 2020-09-12 | 10561.0 | 9406.0 | 9843.0 | 8577.0 | 6544.0 | 4203.0 | 7071.0 | 8550.0 |
| 2020-09-13 | 7183.0 | 10561.0 | 9406.0 | 9843.0 | 8577.0 | 6544.0 | 4203.0 | 7071.0 |
| 2020-09-14 | 6158.0 | 7183.0 | 10561.0 | 9406.0 | 9843.0 | 8577.0 | 6544.0 | 4203.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2021-02-06 | 20586.0 | 22139.0 | 23448.0 | 26362.0 | 23337.0 | 4347.0 | 19235.0 | 24392.0 |
| 2021-02-07 | 19715.0 | 20586.0 | 22139.0 | 23448.0 | 26362.0 | 23337.0 | 4347.0 | 19235.0 |
| 2021-02-08 | 4317.0 | 19715.0 | 20586.0 | 22139.0 | 23448.0 | 26362.0 | 23337.0 | 4347.0 |
| 2021-02-09 | 18870.0 | 4317.0 | 19715.0 | 20586.0 | 22139.0 | 23448.0 | 26362.0 | 23337.0 |
| 2021-02-10 | 25387.0 | 18870.0 | 4317.0 | 19715.0 | 20586.0 | 22139.0 | 23448.0 | 26362.0 |
154 rows × 8 columns
feat = lagged_dataframe(DataFrame({'cas+': data}), 8)
X, y = feat.drop('cas+', axis=1), feat['cas+']
X.shape, y.shape
((154, 7), (154,))
Régression linéaire#
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
lr = make_pipeline(StandardScaler(), LinearRegression())
lr.fit(X, y)
Pipeline(steps=[('standardscaler', StandardScaler()),
('linearregression', LinearRegression())])
from sklearn.metrics import r2_score
r2_score(y, lr.predict(X))
0.639550667481653
r2_score(y, X.values[:, 0])
0.4573617856901514
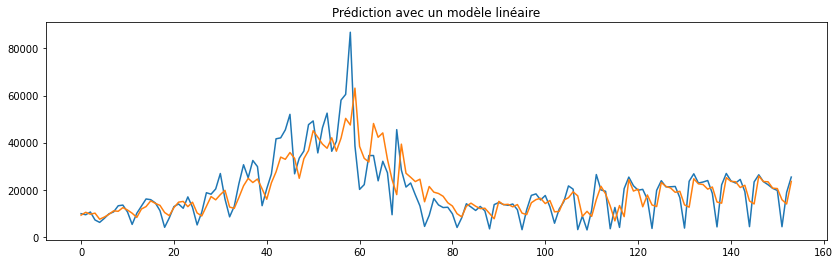
fig, ax = plt.subplots(1, 1, figsize=(14, 4))
ax.plot(y.values)
ax.plot(lr.predict(X))
ax.set_title("Prédiction avec un modèle linéaire");
Autres modèles#
Overfitting ?
from sklearn.model_selection import TimeSeriesSplit
tscv = TimeSeriesSplit(n_splits=5)
for train_index, test_index in tscv.split(X, y):
X_train, X_test, y_train, y_test = (
X.iloc[train_index, :], X.iloc[test_index, :],
y.iloc[train_index], y.iloc[test_index])
print("TRAIN:", X_train.shape, "TEST:", X_test.shape)
TRAIN: (29, 7) TEST: (25, 7)
TRAIN: (54, 7) TEST: (25, 7)
TRAIN: (79, 7) TEST: (25, 7)
TRAIN: (104, 7) TEST: (25, 7)
TRAIN: (129, 7) TEST: (25, 7)