CovidSIRD¶
- class aftercovid.models.CovidSIRD[source]¶
Inspiration Modelling some COVID-19 data.
<<<
from aftercovid.models import CovidSIRD model = CovidSIRD() print(model.to_rst())
>>>
CovidSIRD
Quantities
S: personnes non contaminées
I: nombre de personnes malades ou contaminantes
R: personnes guéries (recovered)
D: personnes décédées
Constants
N: population
Parameters
beta: taux de transmission dans la population
mu: 1/. : durée moyenne jusque la guérison
nu: 1/. : durée moyenne jusqu’au décès
Equations
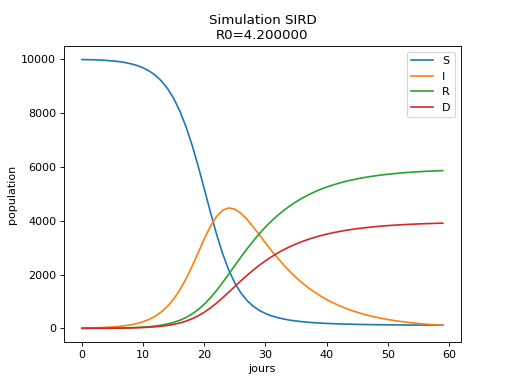
\[\begin{split}\begin{array}{l} \frac{dD}{dt} = I \nu \\ \frac{dI}{dt} = - I \mu - I \nu + \frac{I S \beta}{N} \\ \frac{dR}{dt} = I \mu \\ \frac{dS}{dt} = - \frac{I S \beta}{N} \end{array}\end{split}\]Visual representation:
See Base implementation for SIR models to get the methods common to SIRx models.
- R0(t=0)[source]¶
Returns R0 coefficient.
- Parameters:
t – unused
This coefficients tells how many people one contagious infects in average. Let’s consider the contagious population \(I_t\). A time t+1, there are \(\beta I_t\) new cases and \((\nu + \mu)I_t\) disappear. So at time t+2, there \(\beta I_t(1 - \nu - \mu)\) new cases, at time t+d+1, it is \(\beta I_t(1 - \nu - \mu)^d\). We finally find that: \(R_0=\beta \sum_d (1 - \nu - \mu)^d\) and \(R_0=\frac{\beta}{\nu + \mu}\).