Note
Go to the end to download the full example code
Estimation des paramètres d’un modèle SIRD¶
On part d’un modèle CovidSIRD
qu’on utilise pour simuler des données. On regarde s’il est possible
de réestimer les paramètres du modèle à partir des observations.
Simulation des données¶
import warnings
from pprint import pprint
import numpy
import matplotlib.pyplot as plt
import pandas
from aftercovid.models import EpidemicRegressor, CovidSIRD
model = CovidSIRD()
model
Mise à jour des coefficients.
model['beta'] = 0.4
model["mu"] = 0.06
model["nu"] = 0.04
pprint(model.P)
[('beta', 0.4, 'taux de transmission dans la population'),
('mu', 0.06, '1/. : durée moyenne jusque la guérison'),
('nu', 0.04, "1/. : durée moyenne jusqu'au décès")]
Point de départ
pprint(model.Q)
[('S', 9990.0, 'personnes non contaminées'),
('I', 10.0, 'nombre de personnes malades ou contaminantes'),
('R', 0.0, 'personnes guéries (recovered)'),
('D', 0.0, 'personnes décédées')]
Simulation
Visualisation
df.plot(title="Simulation SIRD")
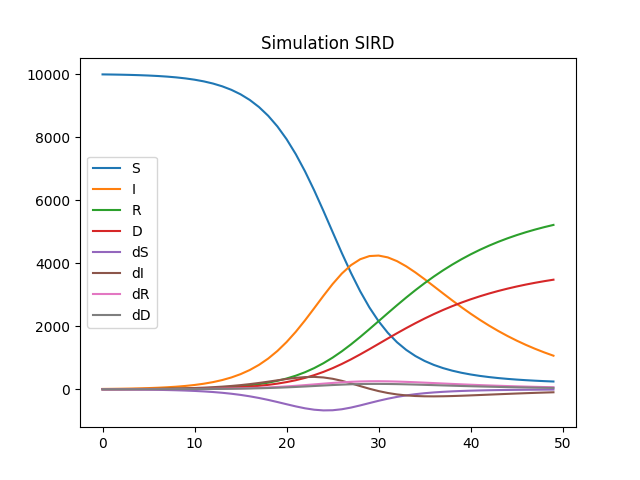
Estimation¶
Le module implémente la class EpidemicRegressor qui réplique
l’API de scikit-learn.
0/10: loss: 1.897e+07 lr=1e-09
1/10: loss: 4.662e+04 lr=1e-09
2/10: loss: 2720 lr=1e-09
3/10: loss: 74.86 lr=1e-09
4/10: loss: 1.046 lr=1e-09
5/10: loss: 0.1211 lr=1e-09
6/10: loss: 0.0005634 lr=1e-09
7/10: loss: 1.639e-05 lr=1e-09
8/10: loss: 5.455e-06 lr=1e-09
9/10: loss: 2.392e-07 lr=1e-09
9/10: loss: 2.392e-07 lr=1e-09 losses: [0.12111801038239137, 0.0005633756116252936, 1.6390378310729972e-05, 5.45491596350498e-06, 2.3921170805405355e-07]
[('beta', 0.40000004594317967, 'taux de transmission dans la population'),
('mu', 0.06000001116898102, '1/. : durée moyenne jusque la guérison'),
('nu', 0.04000001126358509, "1/. : durée moyenne jusqu'au décès")]
La réaction de la population n’est pas constante tout au long de l’épidémie. Il est possible qu’elle change de comportement tout au long de la propagation. On estime alors les coefficients du modèle sur une fenêtre glissante.
def find_best_model(Xt, yt, lrs, th):
best_est, best_loss = None, None
for lr in lrs:
with warnings.catch_warnings():
warnings.simplefilter("ignore", RuntimeWarning)
m = EpidemicRegressor(
'SIRD',
learning_rate_init=lr,
max_iter=500,
early_th=1)
m.fit(Xt, yt)
loss = m.score(Xt, yt)
if numpy.isnan(loss):
continue
if best_est is None or best_loss > loss:
best_est = m
best_loss = loss
if best_loss < th:
return best_est, best_loss
return best_est, best_loss
On estime les coefficients du modèle tous les 2 jours sur les 10 derniers jours.
coefs = []
for k in range(0, X.shape[0] - 9, 2):
end = min(k + 10, X.shape[0])
Xt, yt = X[k:end], y[k:end]
m, loss = find_best_model(Xt, yt, [1e-2, 1e-3], 10)
loss = m.score(Xt, yt)
print(f"k={k} iter={m.iter_} loss={loss:1.3f} coef={m.model_._val_p}")
obs = dict(k=k, loss=loss, it=m.iter_, R0=m.model_.R0())
obs.update({k: v for k, v in zip(m.model_.param_names, m.model_._val_p)})
coefs.append(obs)
k=0 iter=357 loss=2.239 coef=[0.42057372 0.05974595 0.06041957]
k=2 iter=115 loss=0.681 coef=[0.40770366 0.06206369 0.04530839]
k=4 iter=69 loss=0.195 coef=[0.40257024 0.06134319 0.04109677]
k=6 iter=51 loss=0.048 coef=[0.40066258 0.06065819 0.03994949]
k=8 iter=15 loss=0.003 coef=[0.40007427 0.06004131 0.04009177]
k=10 iter=18 loss=0.000 coef=[0.4000037 0.05998615 0.03999451]
k=12 iter=16 loss=0.004 coef=[0.40001642 0.05996604 0.03999531]
k=14 iter=17 loss=0.001 coef=[0.39998623 0.06000873 0.04000317]
k=16 iter=21 loss=0.003 coef=[0.4000189 0.05999387 0.03999535]
k=18 iter=23 loss=0.004 coef=[0.39999899 0.05999656 0.04001737]
k=20 iter=22 loss=0.004 coef=[0.39998931 0.05998449 0.04001077]
k=22 iter=12 loss=4.303 coef=[0.40006285 0.05980054 0.03974741]
k=24 iter=18 loss=0.003 coef=[0.40000538 0.06000393 0.04000789]
k=26 iter=21 loss=0.008 coef=[0.4000625 0.06000895 0.04001048]
k=28 iter=19 loss=0.013 coef=[0.40000717 0.05998938 0.03998689]
k=30 iter=28 loss=0.004 coef=[0.40001303 0.06000733 0.04000734]
k=32 iter=20 loss=0.005 coef=[0.40001409 0.06001034 0.04000935]
k=34 iter=41 loss=0.028 coef=[0.4006094 0.06000335 0.04000336]
k=36 iter=57 loss=0.537 coef=[0.39626394 0.06000206 0.04000206]
k=38 iter=117 loss=3.544 coef=[0.41466743 0.06041745 0.04041745]
k=40 iter=61 loss=13.908 coef=[0.4478056 0.06034639 0.04034639]
Résumé
dfcoef = pandas.DataFrame(coefs).set_index('k')
dfcoef
On visualise.
with warnings.catch_warnings():
warnings.simplefilter("ignore", DeprecationWarning)
fig, ax = plt.subplots(2, 3, figsize=(14, 6))
dfcoef[["mu", "nu"]].plot(ax=ax[0, 0], logy=True)
dfcoef[["beta"]].plot(ax=ax[0, 1], logy=True)
dfcoef[["loss"]].plot(ax=ax[1, 0], logy=True)
dfcoef[["R0"]].plot(ax=ax[0, 2])
df.plot(ax=ax[1, 1], logy=True)
fig.suptitle('Estimation de R0 tout au long de la simulation', fontsize=12)
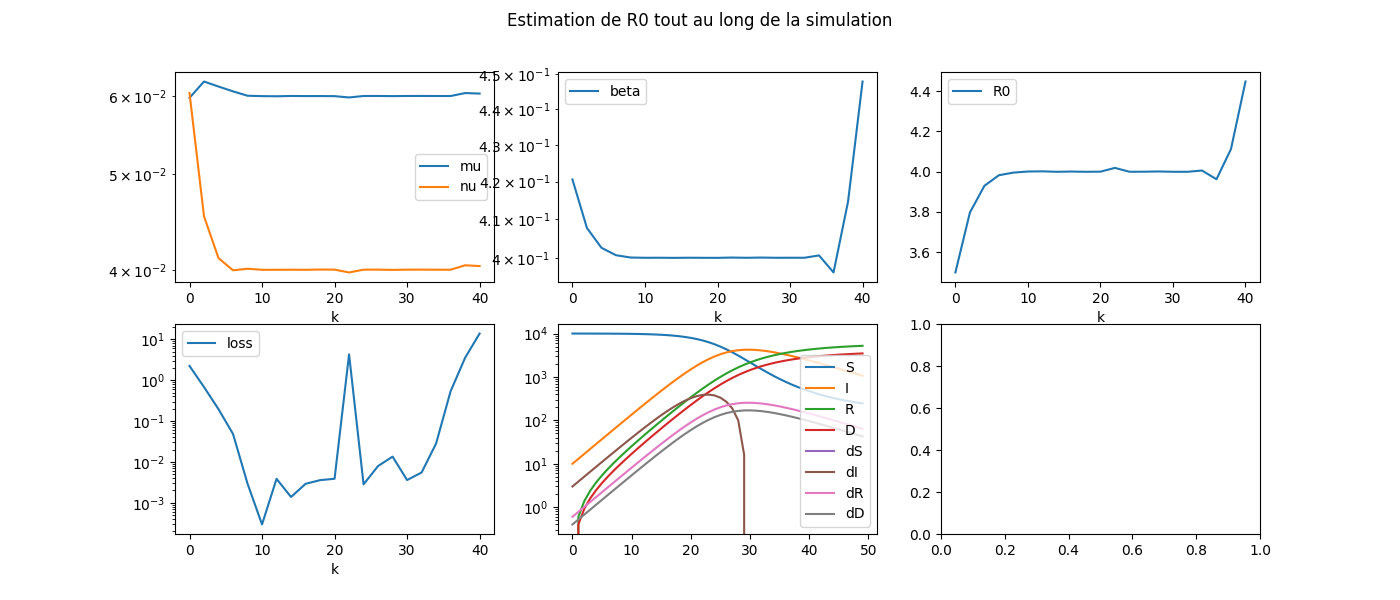
L’estimation des coefficients est plus compliquée au début et à la fin de l’expérience. Il faudrait sans doute changer de stratégie.
Différentes tailles d’estimation¶
Le paramètre beta a été estimé sur une période de 10 jours. Est-ce que cela change sur une période plus courte ou plus longue ? Sur des données parfaites (sans bruit), cela ne devrait pas changer grand chose.
coefs = []
for delay in [4, 5, 6, 7, 8, 9, 10]:
print('delay', delay)
for k in range(0, X.shape[0] - delay, 4):
end = min(k + delay, X.shape[0])
Xt, yt = X[k:end], y[k:end]
m, loss = find_best_model(Xt, yt, [1e-3, 1e-4], 10)
loss = m.score(Xt, yt)
if k == 0:
print(f"k={k} iter={m.iter_} loss={loss:1.3f} "
f"coef={m.model_._val_p}")
obs = dict(k=k, loss=loss, it=m.iter_, R0=m.model_.R0(), delay=delay)
obs.update({k: v for k, v in zip(
m.model_.param_names, m.model_._val_p)})
coefs.append(obs)
delay 4
k=0 iter=5 loss=32.115 coef=[5.89156835e-01 1.20006673e-04 1.18947234e-04]
delay 5
k=0 iter=4 loss=16.496 coef=[0.39504264 0.08779759 0.17077553]
delay 6
k=0 iter=5 loss=14.249 coef=[4.40837922e-01 1.05767498e-04 1.05238477e-04]
delay 7
k=0 iter=5 loss=15.962 coef=[4.21134510e-01 1.07538389e-04 1.06717846e-04]
delay 8
k=0 iter=5 loss=25.134 coef=[4.75745677e-01 1.73788137e-04 1.46194751e-01]
delay 9
k=0 iter=500 loss=43.955 coef=[0.50007395 0.13988022 0.11442095]
delay 10
k=0 iter=500 loss=39.518 coef=[0.49275428 0.08739554 0.11358189]
Résumé
Graphes
with warnings.catch_warnings():
warnings.simplefilter("ignore", DeprecationWarning)
fig, ax = plt.subplots(2, 3, figsize=(14, 6))
for delay in sorted(set(dfcoef['delay'])):
dfcoef.pivot(index='k', columns='delay', values='mu').plot(
ax=ax[0, 0], logy=True, legend=False).set_title('mu')
dfcoef.pivot(index='k', columns='delay', values='nu').plot(
ax=ax[0, 1], logy=True, legend=False).set_title('nu')
dfcoef.pivot(index='k', columns='delay', values='beta').plot(
ax=ax[0, 2], logy=True, legend=False).set_title('beta')
dfcoef.pivot(index='k', columns='delay', values='R0').plot(
ax=ax[1, 2], logy=True, legend=False).set_title('R0')
ax[1, 2].plot([dfcoef.index[0], dfcoef.index[-1]], [1, 1], '--',
label="R0=1")
ax[1, 2].set_ylim(0, 5)
dfcoef.pivot(index='k', columns='delay', values='loss').plot(
ax=ax[1, 0], logy=True, legend=False).set_title('loss')
df.plot(ax=ax[1, 1], logy=True)
fig.suptitle('Estimation de R0 tout au long de la simulation '
'avec différentes tailles de fenêtre', fontsize=12)
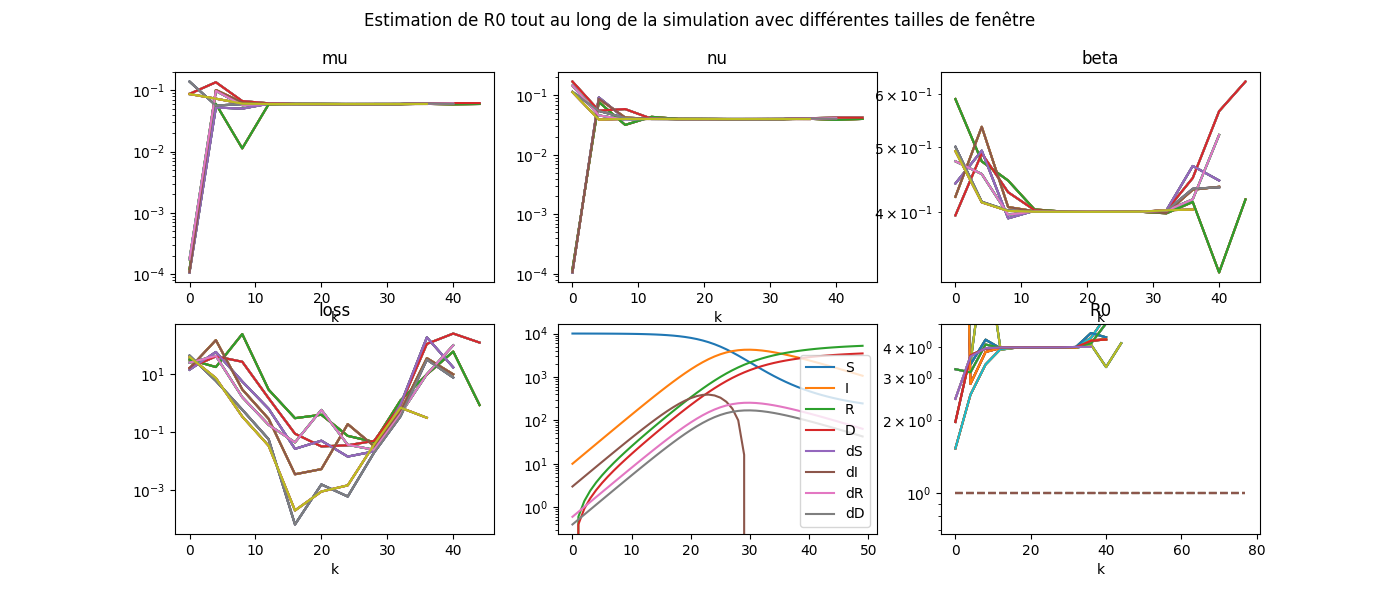
somewhereaftercovid_39_std/aftercovid/examples/plot_covid_estimation.py:191: UserWarning: Attempt to set non-positive ylim on a log-scaled axis will be ignored.
ax[1, 2].set_ylim(0, 5)
somewhereaftercovid_39_std/aftercovid/examples/plot_covid_estimation.py:191: UserWarning: Attempt to set non-positive ylim on a log-scaled axis will be ignored.
ax[1, 2].set_ylim(0, 5)
somewhereaftercovid_39_std/aftercovid/examples/plot_covid_estimation.py:191: UserWarning: Attempt to set non-positive ylim on a log-scaled axis will be ignored.
ax[1, 2].set_ylim(0, 5)
somewhereaftercovid_39_std/aftercovid/examples/plot_covid_estimation.py:191: UserWarning: Attempt to set non-positive ylim on a log-scaled axis will be ignored.
ax[1, 2].set_ylim(0, 5)
somewhereaftercovid_39_std/aftercovid/examples/plot_covid_estimation.py:191: UserWarning: Attempt to set non-positive ylim on a log-scaled axis will be ignored.
ax[1, 2].set_ylim(0, 5)
somewhereaftercovid_39_std/aftercovid/examples/plot_covid_estimation.py:191: UserWarning: Attempt to set non-positive ylim on a log-scaled axis will be ignored.
ax[1, 2].set_ylim(0, 5)
somewhereaftercovid_39_std/aftercovid/examples/plot_covid_estimation.py:191: UserWarning: Attempt to set non-positive ylim on a log-scaled axis will be ignored.
ax[1, 2].set_ylim(0, 5)
Le graphique manque de légende. Ce sera pour plus tard.
Données bruitées¶
L’idée est de voir si l’estimation se comporte aussi bien sur des données bruitées.
On recommence.
coefs = []
for k in range(0, X.shape[0] - 9, 2):
end = min(k + 10, X.shape[0])
Xt, yt = Xeps[k:end], yeps[k:end]
m, loss = find_best_model(Xt, yt, [1e-2, 1e-3, 1e-4], 10)
loss = m.score(Xt, yt)
print(
f"k={k} iter={m.iter_} loss={loss:1.3f} coef={m.model_._val_p}")
obs = dict(k=k, loss=loss, it=m.iter_, R0=m.model_.R0())
obs.update({k: v for k, v in zip(
m.model_.param_names, m.model_._val_p)})
coefs.append(obs)
dfcoef = pandas.DataFrame(coefs).set_index('k')
dfcoef
k=0 iter=201 loss=5.780 coef=[0.41070068 0.07811434 0.03368654]
k=2 iter=171 loss=5.510 coef=[0.39800853 0.0557951 0.05416556]
k=4 iter=63 loss=8.261 coef=[0.39728681 0.05390793 0.05341388]
k=6 iter=43 loss=32.931 coef=[0.40389781 0.060203 0.04468495]
k=8 iter=25 loss=77.128 coef=[0.40437958 0.05255752 0.05316681]
k=10 iter=140 loss=276.834 coef=[0.40840096 0.06288563 0.04039822]
k=12 iter=75 loss=354.680 coef=[0.40832869 0.05782803 0.04400978]
k=14 iter=94 loss=669.593 coef=[0.40700254 0.06373109 0.03444199]
k=16 iter=180 loss=1321.086 coef=[0.40099517 0.06574307 0.03145952]
k=18 iter=168 loss=2374.709 coef=[0.39844081 0.06222821 0.03607916]
k=20 iter=500 loss=3829.429 coef=[0.39937998 0.05792383 0.04200519]
k=22 iter=500 loss=4414.055 coef=[0.40180435 0.06051216 0.04185968]
k=24 iter=500 loss=5441.578 coef=[0.39643104 0.05729299 0.04295057]
k=26 iter=500 loss=7944.976 coef=[0.39229949 0.06049477 0.03897823]
k=28 iter=500 loss=7648.453 coef=[0.4018207 0.06159118 0.03969054]
k=30 iter=500 loss=6708.459 coef=[0.40640136 0.06537355 0.03655733]
k=32 iter=500 loss=4764.194 coef=[0.39701808 0.06753454 0.02698842]
k=34 iter=304 loss=3876.961 coef=[0.34095509 0.06808465 0.02529795]
k=36 iter=500 loss=2729.641 coef=[0.36837205 0.06342619 0.03656187]
k=38 iter=500 loss=2287.201 coef=[0.2733339 0.06438263 0.03290926]
k=40 iter=500 loss=1338.684 coef=[0.27098555 0.05502118 0.03603045]
Graphes.
dfeps = pandas.DataFrame({_[0]: x for _, x in zip(model.Q, Xeps.T)})
with warnings.catch_warnings():
warnings.simplefilter("ignore", DeprecationWarning)
fig, ax = plt.subplots(2, 3, figsize=(14, 6))
dfcoef[["mu", "nu"]].plot(ax=ax[0, 0], logy=True)
dfcoef[["beta"]].plot(ax=ax[0, 1], logy=True)
dfcoef[["loss"]].plot(ax=ax[1, 0], logy=True)
dfcoef[["R0"]].plot(ax=ax[0, 2])
dfeps.plot(ax=ax[1, 1])
fig.suptitle(
'Estimation de R0 tout au long de la simulation sur '
'des données bruitées', fontsize=12)
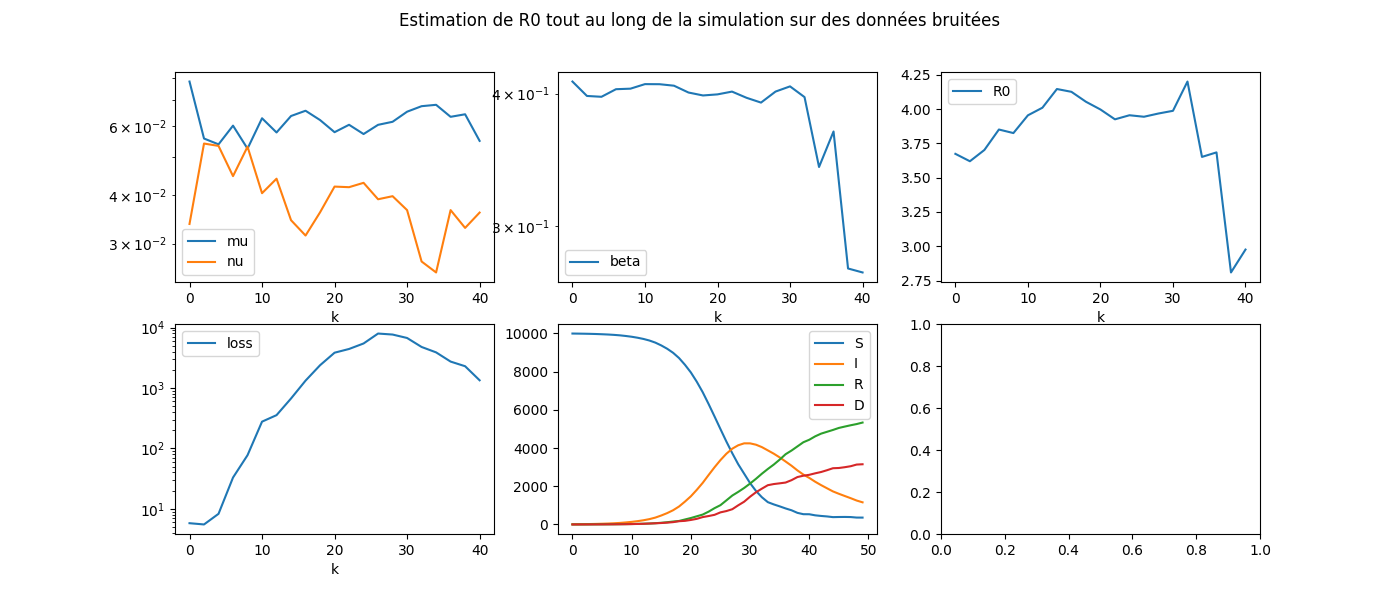
Total running time of the script: ( 4 minutes 10.134 seconds)
