Forward backward on a neural network on GPU

This example leverages example Train a linear regression with onnxruntime-training on GPU in details to train a neural network from scikit-learn on GPU. The code uses the same code introduced in Train a linear regression with forward backward.

A neural network with scikit-learn

import warnings
import numpy
from pandas import DataFrame
from onnxruntime import get_device
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error
from onnxcustom.plotting.plotting_onnx import plot_onnxs
from mlprodict.onnx_conv import to_onnx
from onnxcustom.utils.orttraining_helper import get_train_initializer
from onnxcustom.utils.onnx_helper import onnx_rename_weights
from onnxcustom.training.optimizers_partial import (
    OrtGradientForwardBackwardOptimizer)


X, y = make_regression(1000, n_features=10, bias=2)
X = X.astype(numpy.float32)
y = y.astype(numpy.float32)
X_train, X_test, y_train, y_test = train_test_split(X, y)

nn = MLPRegressor(hidden_layer_sizes=(10, 10), max_iter=100,
                  solver='sgd', learning_rate_init=5e-5,
                  n_iter_no_change=1000, batch_size=10, alpha=0,
                  momentum=0, nesterovs_momentum=False)

with warnings.catch_warnings():
    warnings.simplefilter('ignore')
    nn.fit(X_train, y_train)

print(nn.loss_curve_)

[16672.610546875, 16560.276959635416, 15882.732776692708, 10563.512243652343, 5050.831483256022, 574.1751454671224, 313.5375997924805, 232.1086828104655, 182.2064368693034, 149.1921142578125, 117.04410995483398, 87.2079758199056, 64.2483705774943, 45.84810812632243, 32.44823532104492, 23.301406904856364, 17.20445534388224, 13.230918553670248, 10.854460395177206, 9.229736528396607, 8.117675099372864, 7.205892693201701, 6.558077507019043, 6.035153317848842, 5.553128098249435, 5.2076671846707665, 4.851039233207703, 4.597374379634857, 4.337599027951558, 4.093200965722402, 3.9451861921946207, 3.7354650489489236, 3.570521529515584, 3.4363346870740257, 3.2899771054585774, 3.157844088872274, 3.0404599777857464, 2.916410984992981, 2.8262819465001425, 2.720105598370234, 2.6255326795578005, 2.5208125074704486, 2.434456414381663, 2.3487924567858376, 2.274977253675461, 2.212032690842946, 2.1391211891174318, 2.0823371533552804, 2.0334598263104757, 1.957404642502467, 1.9217858338356018, 1.8669374255339304, 1.812948048512141, 1.779149255355199, 1.7340156320730846, 1.6899153021971385, 1.6511367722352346, 1.6287659740447997, 1.5881430466969808, 1.5528664668401082, 1.5274977441628774, 1.4923988771438599, 1.472212245464325, 1.4330989170074462, 1.4177746669451396, 1.3770861375331878, 1.3351058677832286, 1.3219218897819518, 1.2960139457384745, 1.275530304312706, 1.2432468036810558, 1.2329948961734771, 1.2054487474759419, 1.191846824089686, 1.1775798761844636, 1.1554956610997518, 1.1317561089992523, 1.1128112709522247, 1.0979741044839224, 1.0864841641982397, 1.0655990505218507, 1.05265309492747, 1.0373732882738114, 1.0158864573637645, 1.0067336962620417, 0.999214769800504, 0.9788467444976171, 0.9639906392494837, 0.9506902368863424, 0.9434160772959391, 0.9244991546869278, 0.9220002925395966, 0.9021422656377157, 0.8950206072131792, 0.8875000888109207, 0.876043464342753, 0.8623660150170326, 0.8455535284678142, 0.8427771917978922, 0.8288381878534953]

Score:

print(f"mean_squared_error={mean_squared_error(y_test, nn.predict(X_test))!r}")

mean_squared_error=2.1054227

Conversion to ONNX

onx = to_onnx(nn, X_train[:1].astype(numpy.float32), target_opset=15)
plot_onnxs(onx)

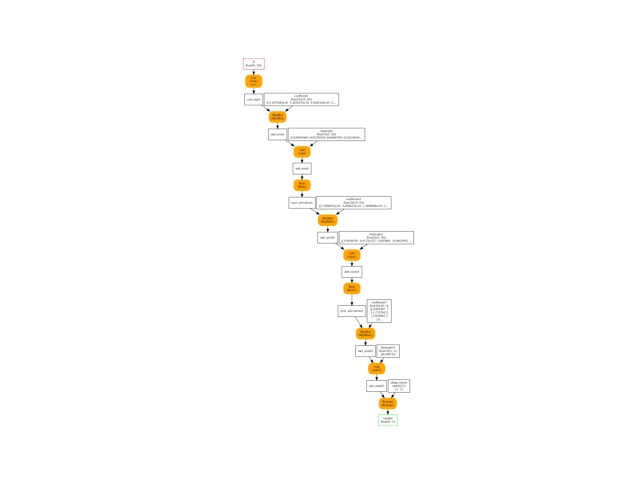
<AxesSubplot: >

Initializers to train

weights = list(sorted(get_train_initializer(onx)))
print(weights)

['coefficient', 'coefficient1', 'coefficient2', 'intercepts', 'intercepts1', 'intercepts2']

Training graph with forward backward

device = "cuda" if get_device().upper() == 'GPU' else 'cpu'

print(f"device={device!r} get_device()={get_device()!r}")

device='cpu' get_device()='CPU'

The training session. The first instructions fails for an odd reason as the class TrainingAgent expects to find the list of weights to train in alphabetical order. That means the list onx.graph.initializer must be sorted by alphabetical order of their names otherwise the process could crash unless it is caught earlier with the following exception.

try:
    train_session = OrtGradientForwardBackwardOptimizer(
        onx, device=device, verbose=1,
        warm_start=False, max_iter=100, batch_size=10)
    train_session.fit(X, y)
except ValueError as e:
    print(e)

List of weights to train must be sorted but ['coefficient', 'intercepts', 'coefficient1', 'intercepts1', 'coefficient2', 'intercepts2'] is not. You shoud use function onnx_rename_weights to do that before calling this class.

Function onnx_rename_weights does not change the order of the initializer but renames them. Then class TrainingAgent may work.

onx = onnx_rename_weights(onx)
train_session = OrtGradientForwardBackwardOptimizer(
    onx, device=device, verbose=1,
    learning_rate=5e-5, warm_start=False, max_iter=100, batch_size=10)
train_session.fit(X, y)

  0%|          | 0/100 [00:00<?, ?it/s]
  1%|1         | 1/100 [00:00<00:17,  5.81it/s]
  2%|2         | 2/100 [00:00<00:15,  6.13it/s]
  3%|3         | 3/100 [00:00<00:15,  6.23it/s]
  4%|4         | 4/100 [00:00<00:15,  6.28it/s]
  5%|5         | 5/100 [00:00<00:15,  6.31it/s]
  6%|6         | 6/100 [00:00<00:14,  6.34it/s]
  7%|7         | 7/100 [00:01<00:14,  6.35it/s]
  8%|8         | 8/100 [00:01<00:14,  6.36it/s]
  9%|9         | 9/100 [00:01<00:14,  6.36it/s]
 10%|#         | 10/100 [00:01<00:14,  6.37it/s]
 11%|#1        | 11/100 [00:01<00:13,  6.38it/s]
 12%|#2        | 12/100 [00:01<00:13,  6.38it/s]
 13%|#3        | 13/100 [00:02<00:13,  6.39it/s]
 14%|#4        | 14/100 [00:02<00:13,  6.39it/s]
 15%|#5        | 15/100 [00:02<00:13,  6.38it/s]
 16%|#6        | 16/100 [00:02<00:13,  6.39it/s]
 17%|#7        | 17/100 [00:02<00:12,  6.39it/s]
 18%|#8        | 18/100 [00:02<00:12,  6.39it/s]
 19%|#9        | 19/100 [00:02<00:12,  6.39it/s]
 20%|##        | 20/100 [00:03<00:12,  6.40it/s]
 21%|##1       | 21/100 [00:03<00:12,  6.40it/s]
 22%|##2       | 22/100 [00:03<00:12,  6.40it/s]
 23%|##3       | 23/100 [00:03<00:12,  6.40it/s]
 24%|##4       | 24/100 [00:03<00:11,  6.39it/s]
 25%|##5       | 25/100 [00:03<00:11,  6.39it/s]
 26%|##6       | 26/100 [00:04<00:11,  6.39it/s]
 27%|##7       | 27/100 [00:04<00:11,  6.40it/s]
 28%|##8       | 28/100 [00:04<00:11,  6.39it/s]
 29%|##9       | 29/100 [00:04<00:11,  6.40it/s]
 30%|###       | 30/100 [00:04<00:10,  6.39it/s]
 31%|###1      | 31/100 [00:04<00:10,  6.39it/s]
 32%|###2      | 32/100 [00:05<00:10,  6.38it/s]
 33%|###3      | 33/100 [00:05<00:10,  6.38it/s]
 34%|###4      | 34/100 [00:05<00:10,  6.37it/s]
 35%|###5      | 35/100 [00:05<00:10,  6.37it/s]
 36%|###6      | 36/100 [00:05<00:10,  6.37it/s]
 37%|###7      | 37/100 [00:05<00:09,  6.37it/s]
 38%|###8      | 38/100 [00:05<00:09,  6.37it/s]
 39%|###9      | 39/100 [00:06<00:09,  6.37it/s]
 40%|####      | 40/100 [00:06<00:09,  6.37it/s]
 41%|####1     | 41/100 [00:06<00:09,  6.37it/s]
 42%|####2     | 42/100 [00:06<00:09,  6.38it/s]
 43%|####3     | 43/100 [00:06<00:08,  6.39it/s]
 44%|####4     | 44/100 [00:06<00:08,  6.39it/s]
 45%|####5     | 45/100 [00:07<00:08,  6.39it/s]
 46%|####6     | 46/100 [00:07<00:08,  6.39it/s]
 47%|####6     | 47/100 [00:07<00:08,  6.38it/s]
 48%|####8     | 48/100 [00:07<00:08,  6.39it/s]
 49%|####9     | 49/100 [00:07<00:07,  6.38it/s]
 50%|#####     | 50/100 [00:07<00:07,  6.38it/s]
 51%|#####1    | 51/100 [00:08<00:07,  6.38it/s]
 52%|#####2    | 52/100 [00:08<00:07,  6.37it/s]
 53%|#####3    | 53/100 [00:08<00:07,  6.38it/s]
 54%|#####4    | 54/100 [00:08<00:07,  6.38it/s]
 55%|#####5    | 55/100 [00:08<00:07,  6.38it/s]
 56%|#####6    | 56/100 [00:08<00:06,  6.38it/s]
 57%|#####6    | 57/100 [00:08<00:06,  6.38it/s]
 58%|#####8    | 58/100 [00:09<00:06,  6.39it/s]
 59%|#####8    | 59/100 [00:09<00:06,  6.38it/s]
 60%|######    | 60/100 [00:09<00:06,  6.38it/s]
 61%|######1   | 61/100 [00:09<00:06,  6.40it/s]
 62%|######2   | 62/100 [00:09<00:05,  6.39it/s]
 63%|######3   | 63/100 [00:09<00:05,  6.39it/s]
 64%|######4   | 64/100 [00:10<00:05,  6.39it/s]
 65%|######5   | 65/100 [00:10<00:05,  6.39it/s]
 66%|######6   | 66/100 [00:10<00:05,  6.39it/s]
 67%|######7   | 67/100 [00:10<00:05,  6.39it/s]
 68%|######8   | 68/100 [00:10<00:05,  6.39it/s]
 69%|######9   | 69/100 [00:10<00:04,  6.38it/s]
 70%|#######   | 70/100 [00:10<00:04,  6.39it/s]
 71%|#######1  | 71/100 [00:11<00:04,  6.39it/s]
 72%|#######2  | 72/100 [00:11<00:04,  6.39it/s]
 73%|#######3  | 73/100 [00:11<00:04,  6.39it/s]
 74%|#######4  | 74/100 [00:11<00:04,  6.39it/s]
 75%|#######5  | 75/100 [00:11<00:03,  6.40it/s]
 76%|#######6  | 76/100 [00:11<00:03,  6.39it/s]
 77%|#######7  | 77/100 [00:12<00:03,  6.39it/s]
 78%|#######8  | 78/100 [00:12<00:03,  6.39it/s]
 79%|#######9  | 79/100 [00:12<00:03,  6.39it/s]
 80%|########  | 80/100 [00:12<00:03,  6.39it/s]
 81%|########1 | 81/100 [00:12<00:02,  6.39it/s]
 82%|########2 | 82/100 [00:12<00:02,  6.39it/s]
 83%|########2 | 83/100 [00:13<00:02,  6.39it/s]
 84%|########4 | 84/100 [00:13<00:02,  6.39it/s]
 85%|########5 | 85/100 [00:13<00:02,  6.39it/s]
 86%|########6 | 86/100 [00:13<00:02,  6.39it/s]
 87%|########7 | 87/100 [00:13<00:02,  6.39it/s]
 88%|########8 | 88/100 [00:13<00:01,  6.39it/s]
 89%|########9 | 89/100 [00:13<00:01,  6.39it/s]
 90%|######### | 90/100 [00:14<00:01,  6.39it/s]
 91%|#########1| 91/100 [00:14<00:01,  6.39it/s]
 92%|#########2| 92/100 [00:14<00:01,  6.38it/s]
 93%|#########3| 93/100 [00:14<00:01,  6.38it/s]
 94%|#########3| 94/100 [00:14<00:00,  6.38it/s]
 95%|#########5| 95/100 [00:14<00:00,  6.39it/s]
 96%|#########6| 96/100 [00:15<00:00,  6.39it/s]
 97%|#########7| 97/100 [00:15<00:00,  6.39it/s]
 98%|#########8| 98/100 [00:15<00:00,  6.38it/s]
 99%|#########9| 99/100 [00:15<00:00,  6.39it/s]
100%|##########| 100/100 [00:15<00:00,  6.38it/s]
100%|##########| 100/100 [00:15<00:00,  6.38it/s]

OrtGradientForwardBackwardOptimizer(model_onnx='ir_version...', weights_to_train="['I0_coeff...", loss_output_name='loss', max_iter=100, training_optimizer_name='SGDOptimizer', batch_size=10, learning_rate=LearningRateSGD(eta0=5e-05, alpha=0.0001, power_t=0.25, learning_rate='invscaling'), value=1.5811388300841898e-05, device='cpu', warm_start=False, verbose=1, validation_every=10, learning_loss=SquareLearningLoss(), enable_logging=False, weight_name=None, learning_penalty=NoLearningPenalty(), exc=True)

Let’s see the weights.

state_tensors = train_session.get_state()

And the loss.

print(train_session.train_losses_)

df = DataFrame({'ort losses': train_session.train_losses_,
                'skl losses:': nn.loss_curve_})
df.plot(title="Train loss against iterations", logy=True)

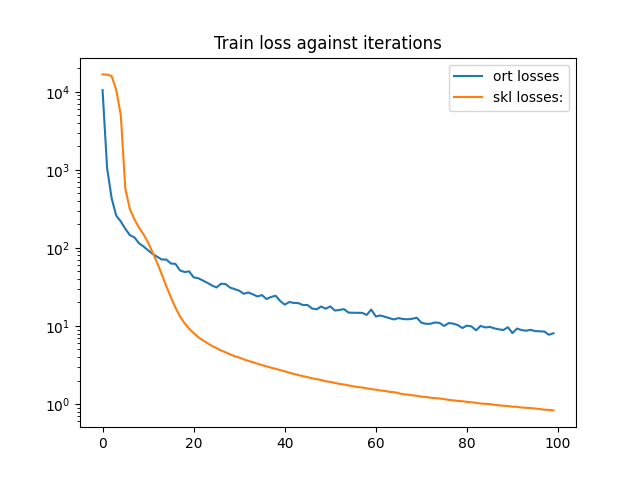
[10486.421, 1054.1023, 430.22656, 259.36642, 217.79132, 175.79523, 145.47513, 136.30801, 114.48367, 104.36836, 93.13665, 83.576416, 76.9638, 71.03061, 70.90978, 63.078568, 62.396793, 51.506927, 49.051544, 50.006573, 41.948753, 40.886585, 38.2834, 35.725277, 33.04002, 31.098604, 34.714676, 34.429195, 31.00148, 29.628838, 28.314756, 25.84481, 26.83611, 25.429285, 23.85272, 24.841177, 22.122534, 23.51305, 24.383778, 20.89044, 18.766773, 20.252422, 19.728455, 19.634481, 18.512548, 18.558884, 16.71529, 16.35347, 17.731834, 16.620045, 17.802332, 15.745441, 16.016972, 16.426186, 14.823928, 14.773128, 14.727218, 14.720404, 13.856672, 16.224731, 13.228546, 13.632607, 13.096942, 12.5659485, 12.11636, 12.608312, 12.261661, 12.166393, 12.372383, 12.726557, 11.011409, 10.651968, 10.669263, 11.0856495, 10.945174, 9.995138, 10.894199, 10.710474, 10.264939, 9.417556, 10.1014805, 9.869503, 8.797937, 10.021265, 9.562256, 9.736806, 9.322936, 9.051759, 8.873677, 9.637808, 8.1019745, 9.267523, 8.850331, 8.697312, 8.920007, 8.597367, 8.538077, 8.476014, 7.7139764, 8.063694]

<AxesSubplot: title={'center': 'Train loss against iterations'}>

The convergence rate is different but both classes do not update the learning the same way.

# import matplotlib.pyplot as plt
# plt.show()