Note
Click here to download the full example code
Forward backward on a neural network on GPU (Nesterov) and penalty#
This example does the same as Forward backward on a neural network on GPU but updates the weights using Nesterov momentum.
A neural network with scikit-learn#
import warnings
import numpy
import onnx
from pandas import DataFrame
from onnxruntime import get_device
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error
from onnxcustom.plotting.plotting_onnx import plot_onnxs
from mlprodict.onnx_conv import to_onnx
from mlprodict.plotting.text_plot import onnx_simple_text_plot
from onnxcustom.utils.orttraining_helper import get_train_initializer
from onnxcustom.utils.onnx_helper import onnx_rename_weights
from onnxcustom.training.optimizers_partial import (
OrtGradientForwardBackwardOptimizer)
from onnxcustom.training.sgd_learning_rate import LearningRateSGDNesterov
from onnxcustom.training.sgd_learning_penalty import ElasticLearningPenalty
X, y = make_regression(1000, n_features=10, bias=2)
X = X.astype(numpy.float32)
y = y.astype(numpy.float32)
X_train, X_test, y_train, y_test = train_test_split(X, y)
nn = MLPRegressor(hidden_layer_sizes=(10, 10), max_iter=100,
solver='sgd', learning_rate_init=5e-5,
n_iter_no_change=1000, batch_size=10, alpha=0,
momentum=0.9, nesterovs_momentum=True)
with warnings.catch_warnings():
warnings.simplefilter('ignore')
nn.fit(X_train, y_train)
print(nn.loss_curve_)
[16727.14858642578, 9886.648673095704, 9645.244761149088, 9427.457867094676, 9216.884807535807, 9015.537370198568, 8819.54773768107, 8630.19841451009, 8447.27973180135, 8269.965132141113, 4625.528131306966, 19.894860242207844, 2.5911614493529003, 1.8056361218293508, 1.5604278735319774, 1.1023686797420185, 0.9809801054994265, 0.8389275055130323, 0.7330209936698278, 0.6682993817826112, 0.5586919712523619, 0.5553150833149751, 0.506476029753685, 0.44125502961377305, 0.4403625219066938, 0.41900782456000646, 0.3498478382329146, 0.33808369780580205, 0.3388243389129639, 0.3201561619589726, 0.2968847231318553, 0.25809116010864575, 0.25949058794726926, 0.24270301714539527, 0.24118004883329072, 0.2241997817903757, 0.23721586545308432, 0.20840331830084324, 0.209505176966389, 0.19847349734356007, 0.18222187149027982, 0.1801910589138667, 0.16816076944271724, 0.16541445123652618, 0.15733496909340222, 0.1545709479600191, 0.14522852240751186, 0.13618677285810313, 0.14466529297331968, 0.14250882079203925, 0.1329341151068608, 0.12472076637049516, 0.12226070703317722, 0.11392398949712515, 0.11658183907469113, 0.10829457469905417, 0.11358472261577844, 0.1039104288816452, 0.10292356649413704, 0.1054613478668034, 0.10019272891183695, 0.09628251068294048, 0.08810045094539722, 0.09373769973715146, 0.091689777597785, 0.08503272091348966, 0.08667534582316876, 0.08453616673747698, 0.07860475547611713, 0.07970112061748902, 0.07944699289898077, 0.07488435259709755, 0.07543826389436921, 0.07364978392298023, 0.07391809318214655, 0.06721652362495661, 0.06525374284790209, 0.06821930796528856, 0.06798541801671187, 0.06362760667378704, 0.06456263530999422, 0.06274791978299618, 0.06577064234142502, 0.06174186892807484, 0.060641947615270815, 0.05955235173304876, 0.05593090050543348, 0.056281895929326614, 0.05896102330336968, 0.05452152626588941, 0.053325654889146486, 0.051699511824796596, 0.05203500121831894, 0.051343476992721356, 0.051559900312374035, 0.047762058998147644, 0.047344295202443994, 0.04345790034160018, 0.044110719859600064, 0.0450264458078891]
Score:
print(f"mean_squared_error={mean_squared_error(y_test, nn.predict(X_test))!r}")
mean_squared_error=0.37034693
Conversion to ONNX#
onx = to_onnx(nn, X_train[:1].astype(numpy.float32), target_opset=15)
plot_onnxs(onx)
weights = list(sorted(get_train_initializer(onx)))
print(weights)
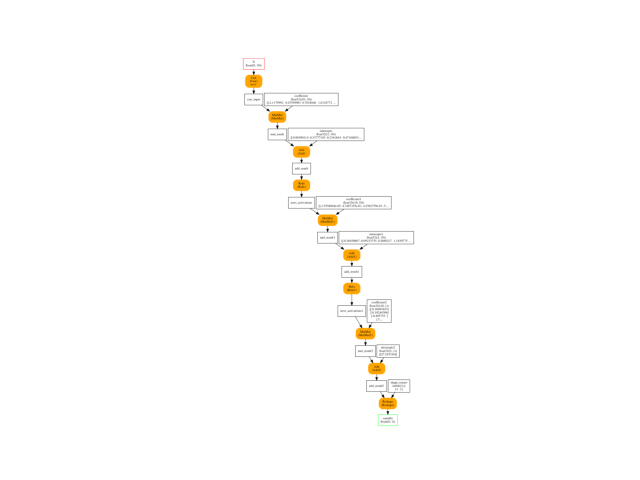
['coefficient', 'coefficient1', 'coefficient2', 'intercepts', 'intercepts1', 'intercepts2']
Training graph with forward backward#
device = "cuda" if get_device().upper() == 'GPU' else 'cpu'
print(f"device={device!r} get_device()={get_device()!r}")
onx = onnx_rename_weights(onx)
train_session = OrtGradientForwardBackwardOptimizer(
onx, device=device, verbose=1,
learning_rate=LearningRateSGDNesterov(1e-4, nesterov=True, momentum=0.9),
warm_start=False, max_iter=100, batch_size=10)
train_session.fit(X, y)
device='cpu' get_device()='CPU'
0%| | 0/100 [00:00<?, ?it/s]
1%|1 | 1/100 [00:00<00:19, 5.08it/s]
2%|2 | 2/100 [00:00<00:18, 5.25it/s]
3%|3 | 3/100 [00:00<00:18, 5.31it/s]
4%|4 | 4/100 [00:00<00:17, 5.34it/s]
5%|5 | 5/100 [00:00<00:17, 5.34it/s]
6%|6 | 6/100 [00:01<00:17, 5.35it/s]
7%|7 | 7/100 [00:01<00:17, 5.35it/s]
8%|8 | 8/100 [00:01<00:17, 5.35it/s]
9%|9 | 9/100 [00:01<00:17, 5.35it/s]
10%|# | 10/100 [00:01<00:16, 5.35it/s]
11%|#1 | 11/100 [00:02<00:16, 5.35it/s]
12%|#2 | 12/100 [00:02<00:16, 5.36it/s]
13%|#3 | 13/100 [00:02<00:16, 5.38it/s]
14%|#4 | 14/100 [00:02<00:15, 5.38it/s]
15%|#5 | 15/100 [00:02<00:15, 5.38it/s]
16%|#6 | 16/100 [00:02<00:15, 5.39it/s]
17%|#7 | 17/100 [00:03<00:15, 5.40it/s]
18%|#8 | 18/100 [00:03<00:15, 5.40it/s]
19%|#9 | 19/100 [00:03<00:14, 5.40it/s]
20%|## | 20/100 [00:03<00:14, 5.40it/s]
21%|##1 | 21/100 [00:03<00:14, 5.41it/s]
22%|##2 | 22/100 [00:04<00:14, 5.41it/s]
23%|##3 | 23/100 [00:04<00:14, 5.41it/s]
24%|##4 | 24/100 [00:04<00:14, 5.41it/s]
25%|##5 | 25/100 [00:04<00:13, 5.41it/s]
26%|##6 | 26/100 [00:04<00:13, 5.41it/s]
27%|##7 | 27/100 [00:05<00:13, 5.40it/s]
28%|##8 | 28/100 [00:05<00:13, 5.40it/s]
29%|##9 | 29/100 [00:05<00:13, 5.40it/s]
30%|### | 30/100 [00:05<00:12, 5.41it/s]
31%|###1 | 31/100 [00:05<00:12, 5.41it/s]
32%|###2 | 32/100 [00:05<00:12, 5.40it/s]
33%|###3 | 33/100 [00:06<00:12, 5.40it/s]
34%|###4 | 34/100 [00:06<00:12, 5.40it/s]
35%|###5 | 35/100 [00:06<00:12, 5.41it/s]
36%|###6 | 36/100 [00:06<00:11, 5.40it/s]
37%|###7 | 37/100 [00:06<00:11, 5.40it/s]
38%|###8 | 38/100 [00:07<00:11, 5.40it/s]
39%|###9 | 39/100 [00:07<00:11, 5.41it/s]
40%|#### | 40/100 [00:07<00:11, 5.40it/s]
41%|####1 | 41/100 [00:07<00:10, 5.40it/s]
42%|####2 | 42/100 [00:07<00:10, 5.41it/s]
43%|####3 | 43/100 [00:07<00:10, 5.40it/s]
44%|####4 | 44/100 [00:08<00:10, 5.40it/s]
45%|####5 | 45/100 [00:08<00:10, 5.40it/s]
46%|####6 | 46/100 [00:08<00:09, 5.40it/s]
47%|####6 | 47/100 [00:08<00:09, 5.40it/s]
48%|####8 | 48/100 [00:08<00:09, 5.40it/s]
49%|####9 | 49/100 [00:09<00:09, 5.39it/s]
50%|##### | 50/100 [00:09<00:09, 5.40it/s]
51%|#####1 | 51/100 [00:09<00:09, 5.40it/s]
52%|#####2 | 52/100 [00:09<00:08, 5.39it/s]
53%|#####3 | 53/100 [00:09<00:08, 5.38it/s]
54%|#####4 | 54/100 [00:10<00:08, 5.38it/s]
55%|#####5 | 55/100 [00:10<00:08, 5.39it/s]
56%|#####6 | 56/100 [00:10<00:08, 5.39it/s]
57%|#####6 | 57/100 [00:10<00:07, 5.40it/s]
58%|#####8 | 58/100 [00:10<00:07, 5.40it/s]
59%|#####8 | 59/100 [00:10<00:07, 5.40it/s]
60%|###### | 60/100 [00:11<00:07, 5.40it/s]
61%|######1 | 61/100 [00:11<00:07, 5.40it/s]
62%|######2 | 62/100 [00:11<00:07, 5.40it/s]
63%|######3 | 63/100 [00:11<00:06, 5.40it/s]
64%|######4 | 64/100 [00:11<00:06, 5.41it/s]
65%|######5 | 65/100 [00:12<00:06, 5.40it/s]
66%|######6 | 66/100 [00:12<00:06, 5.40it/s]
67%|######7 | 67/100 [00:12<00:06, 5.41it/s]
68%|######8 | 68/100 [00:12<00:05, 5.42it/s]
69%|######9 | 69/100 [00:12<00:05, 5.41it/s]
70%|####### | 70/100 [00:12<00:05, 5.40it/s]
71%|#######1 | 71/100 [00:13<00:05, 5.41it/s]
72%|#######2 | 72/100 [00:13<00:05, 5.40it/s]
73%|#######3 | 73/100 [00:13<00:04, 5.41it/s]
74%|#######4 | 74/100 [00:13<00:04, 5.40it/s]
75%|#######5 | 75/100 [00:13<00:04, 5.40it/s]
76%|#######6 | 76/100 [00:14<00:04, 5.40it/s]
77%|#######7 | 77/100 [00:14<00:04, 5.39it/s]
78%|#######8 | 78/100 [00:14<00:04, 5.40it/s]
79%|#######9 | 79/100 [00:14<00:03, 5.41it/s]
80%|######## | 80/100 [00:14<00:03, 5.41it/s]
81%|########1 | 81/100 [00:15<00:03, 5.40it/s]
82%|########2 | 82/100 [00:15<00:03, 5.40it/s]
83%|########2 | 83/100 [00:15<00:03, 5.39it/s]
84%|########4 | 84/100 [00:15<00:02, 5.39it/s]
85%|########5 | 85/100 [00:15<00:02, 5.38it/s]
86%|########6 | 86/100 [00:15<00:02, 5.38it/s]
87%|########7 | 87/100 [00:16<00:02, 5.38it/s]
88%|########8 | 88/100 [00:16<00:02, 5.39it/s]
89%|########9 | 89/100 [00:16<00:02, 5.40it/s]
90%|######### | 90/100 [00:16<00:01, 5.39it/s]
91%|#########1| 91/100 [00:16<00:01, 5.38it/s]
92%|#########2| 92/100 [00:17<00:01, 5.38it/s]
93%|#########3| 93/100 [00:17<00:01, 5.38it/s]
94%|#########3| 94/100 [00:17<00:01, 5.38it/s]
95%|#########5| 95/100 [00:17<00:00, 5.38it/s]
96%|#########6| 96/100 [00:17<00:00, 5.37it/s]
97%|#########7| 97/100 [00:17<00:00, 5.37it/s]
98%|#########8| 98/100 [00:18<00:00, 5.38it/s]
99%|#########9| 99/100 [00:18<00:00, 5.39it/s]
100%|##########| 100/100 [00:18<00:00, 5.39it/s]
100%|##########| 100/100 [00:18<00:00, 5.39it/s]
OrtGradientForwardBackwardOptimizer(model_onnx='ir_version...', weights_to_train="['I0_coeff...", loss_output_name='loss', max_iter=100, training_optimizer_name='SGDOptimizer', batch_size=10, learning_rate=LearningRateSGDNesterov(eta0=0.0001, alpha=0.0001, power_t=0.25, learning_rate='invscaling', momentum=0.9, nesterov=True), value=3.1622776601683795e-05, device='cpu', warm_start=False, verbose=1, validation_every=10, learning_loss=SquareLearningLoss(), enable_logging=False, weight_name=None, learning_penalty=NoLearningPenalty(), exc=True)
Let’s see the weights.
state_tensors = train_session.get_state()
And the loss.
print(train_session.train_losses_)
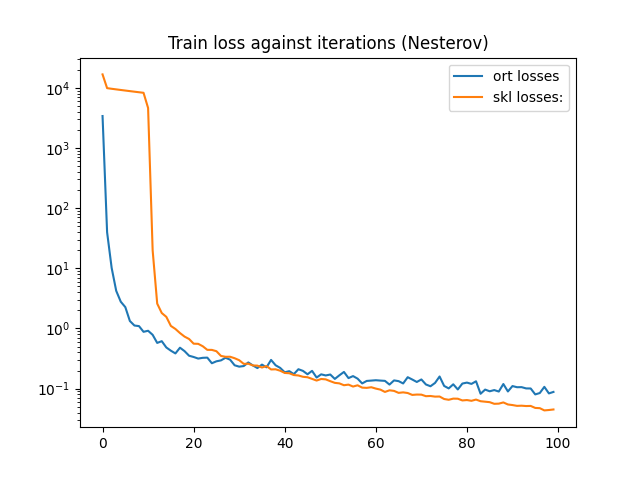
df = DataFrame({'ort losses': train_session.train_losses_,
'skl losses:': nn.loss_curve_})
df.plot(title="Train loss against iterations (Nesterov)", logy=True)
[3399.0227, 39.741074, 10.149199, 4.224396, 2.7856283, 2.2636168, 1.3312259, 1.119156, 1.0948006, 0.8801888, 0.91582054, 0.7840815, 0.5753221, 0.6149931, 0.48320496, 0.42714757, 0.38476792, 0.47893086, 0.42041075, 0.3522385, 0.33559498, 0.3160123, 0.32519352, 0.32763538, 0.26415843, 0.28451484, 0.29470086, 0.32584983, 0.30322552, 0.2444154, 0.23185429, 0.23742177, 0.27236935, 0.24306953, 0.21959709, 0.25082037, 0.22615182, 0.30005848, 0.24439558, 0.22118339, 0.1868661, 0.1951086, 0.17423186, 0.21018668, 0.19721217, 0.17329422, 0.19738458, 0.15287174, 0.17285597, 0.16556582, 0.17153835, 0.14502455, 0.16657801, 0.18935204, 0.14961125, 0.16161941, 0.14649294, 0.12198622, 0.13423161, 0.13601989, 0.13792156, 0.13610159, 0.13459037, 0.11676124, 0.1370015, 0.13318574, 0.121905595, 0.15485296, 0.14170673, 0.12902437, 0.142034, 0.11722834, 0.10950032, 0.12430995, 0.15907623, 0.1108771, 0.10083976, 0.1179764, 0.09685761, 0.12140604, 0.12590106, 0.11986154, 0.13248257, 0.08215951, 0.09637261, 0.090318136, 0.09461293, 0.0894553, 0.11927412, 0.08974456, 0.11030881, 0.10556896, 0.10583564, 0.100795634, 0.10058017, 0.08016467, 0.0844858, 0.10700203, 0.083273165, 0.0881392]
<AxesSubplot: title={'center': 'Train loss against iterations (Nesterov)'}>
The convergence rate is different but both classes do not update the learning exactly the same way.
Regularization#
Default parameters for MLPRegressor suggest to penalize weights during training: alpha=1e-4.
nn = MLPRegressor(hidden_layer_sizes=(10, 10), max_iter=100,
solver='sgd', learning_rate_init=5e-5,
n_iter_no_change=1000, batch_size=10, alpha=1e-4,
momentum=0.9, nesterovs_momentum=True)
with warnings.catch_warnings():
warnings.simplefilter('ignore')
nn.fit(X_train, y_train)
print(nn.loss_curve_)
[16644.470284628394, 401.1068514653827, 6.738641275841776, 3.9318541452701568, 3.0244461122994744, 2.2532218629456837, 1.9772367759969083, 1.5282178701265021, 1.2223396551051453, 1.1481130557331083, 1.0134906597261433, 0.8003500148251053, 0.7748838875124933, 0.7247065508871078, 0.6424079205564815, 0.5943848107209843, 0.553769108420817, 0.48247862568184535, 0.43316434307597496, 0.41002364917958567, 0.38026980786356124, 0.3443462980669339, 0.3342713889621418, 0.30697219307897894, 0.3016236751692852, 0.2895430512654464, 0.25963947670109255, 0.23793626513503394, 0.2492147737905185, 0.23493280009342823, 0.22015180201351656, 0.21636547789567312, 0.18563474208073616, 0.1842764515189648, 0.17788540328239605, 0.18060155422696275, 0.15780622708411216, 0.16003681248737178, 0.1588067330984592, 0.15432866777893697, 0.15216210509080888, 0.13951552215674717, 0.12728950660916163, 0.12945707742733162, 0.11697847371650143, 0.11847423953349, 0.11704880033358732, 0.11336992760983704, 0.11430779519991084, 0.10544585204260545, 0.10479470225338534, 0.09545615410556399, 0.10430054900427659, 0.09535739087892374, 0.09120253478180174, 0.09298379923061131, 0.08554529027584395, 0.09110059936119713, 0.08243054630705117, 0.0785640923050801, 0.08334481671629546, 0.07713220271193584, 0.08134272320773601, 0.0736682232308825, 0.07106144472306963, 0.06550185541106761, 0.06746809417481027, 0.06551346430557567, 0.06398837047621408, 0.0632499319100062, 0.06220720928388039, 0.0571461602373769, 0.055784664296476064, 0.05701089259317717, 0.05496140191216072, 0.05264682256058155, 0.05429102085848053, 0.04971476362698874, 0.05152108289290767, 0.050431329947054376, 0.05051382197133403, 0.04627255402097006, 0.04662131737909318, 0.04366316913842857, 0.04362656782296103, 0.04168388342069487, 0.04351087063009739, 0.039616904199122394, 0.041562781108266125, 0.03999037445789874, 0.04018290116106272, 0.0379325491681973, 0.03792251015276213, 0.03627130159715811, 0.03842348616118133, 0.03541234316809575, 0.03555839157693685, 0.035423021728076556, 0.034860185407544174, 0.03410663728183011]
Let’s do the same with onnxruntime.
train_session = OrtGradientForwardBackwardOptimizer(
onx, device=device, verbose=1,
learning_rate=LearningRateSGDNesterov(1e-4, nesterov=True, momentum=0.9),
learning_penalty=ElasticLearningPenalty(l1=0, l2=1e-4),
warm_start=False, max_iter=100, batch_size=10)
train_session.fit(X, y)
0%| | 0/100 [00:00<?, ?it/s]
1%|1 | 1/100 [00:00<00:25, 3.94it/s]
2%|2 | 2/100 [00:00<00:25, 3.92it/s]
3%|3 | 3/100 [00:00<00:24, 3.92it/s]
4%|4 | 4/100 [00:01<00:24, 3.90it/s]
5%|5 | 5/100 [00:01<00:24, 3.91it/s]
6%|6 | 6/100 [00:01<00:24, 3.90it/s]
7%|7 | 7/100 [00:01<00:23, 3.90it/s]
8%|8 | 8/100 [00:02<00:23, 3.91it/s]
9%|9 | 9/100 [00:02<00:23, 3.91it/s]
10%|# | 10/100 [00:02<00:23, 3.90it/s]
11%|#1 | 11/100 [00:02<00:22, 3.90it/s]
12%|#2 | 12/100 [00:03<00:22, 3.90it/s]
13%|#3 | 13/100 [00:03<00:22, 3.90it/s]
14%|#4 | 14/100 [00:03<00:22, 3.91it/s]
15%|#5 | 15/100 [00:03<00:21, 3.91it/s]
16%|#6 | 16/100 [00:04<00:21, 3.91it/s]
17%|#7 | 17/100 [00:04<00:21, 3.91it/s]
18%|#8 | 18/100 [00:04<00:21, 3.90it/s]
19%|#9 | 19/100 [00:04<00:20, 3.90it/s]
20%|## | 20/100 [00:05<00:20, 3.90it/s]
21%|##1 | 21/100 [00:05<00:20, 3.90it/s]
22%|##2 | 22/100 [00:05<00:19, 3.90it/s]
23%|##3 | 23/100 [00:05<00:19, 3.90it/s]
24%|##4 | 24/100 [00:06<00:19, 3.89it/s]
25%|##5 | 25/100 [00:06<00:19, 3.90it/s]
26%|##6 | 26/100 [00:06<00:19, 3.89it/s]
27%|##7 | 27/100 [00:06<00:18, 3.89it/s]
28%|##8 | 28/100 [00:07<00:18, 3.89it/s]
29%|##9 | 29/100 [00:07<00:18, 3.90it/s]
30%|### | 30/100 [00:07<00:17, 3.90it/s]
31%|###1 | 31/100 [00:07<00:17, 3.90it/s]
32%|###2 | 32/100 [00:08<00:17, 3.89it/s]
33%|###3 | 33/100 [00:08<00:17, 3.89it/s]
34%|###4 | 34/100 [00:08<00:16, 3.89it/s]
35%|###5 | 35/100 [00:08<00:16, 3.89it/s]
36%|###6 | 36/100 [00:09<00:16, 3.89it/s]
37%|###7 | 37/100 [00:09<00:16, 3.89it/s]
38%|###8 | 38/100 [00:09<00:15, 3.90it/s]
39%|###9 | 39/100 [00:09<00:15, 3.90it/s]
40%|#### | 40/100 [00:10<00:15, 3.90it/s]
41%|####1 | 41/100 [00:10<00:15, 3.89it/s]
42%|####2 | 42/100 [00:10<00:14, 3.89it/s]
43%|####3 | 43/100 [00:11<00:14, 3.90it/s]
44%|####4 | 44/100 [00:11<00:14, 3.90it/s]
45%|####5 | 45/100 [00:11<00:14, 3.90it/s]
46%|####6 | 46/100 [00:11<00:13, 3.91it/s]
47%|####6 | 47/100 [00:12<00:13, 3.91it/s]
48%|####8 | 48/100 [00:12<00:13, 3.91it/s]
49%|####9 | 49/100 [00:12<00:13, 3.90it/s]
50%|##### | 50/100 [00:12<00:12, 3.89it/s]
51%|#####1 | 51/100 [00:13<00:12, 3.90it/s]
52%|#####2 | 52/100 [00:13<00:12, 3.90it/s]
53%|#####3 | 53/100 [00:13<00:12, 3.90it/s]
54%|#####4 | 54/100 [00:13<00:11, 3.90it/s]
55%|#####5 | 55/100 [00:14<00:11, 3.90it/s]
56%|#####6 | 56/100 [00:14<00:11, 3.91it/s]
57%|#####6 | 57/100 [00:14<00:10, 3.91it/s]
58%|#####8 | 58/100 [00:14<00:10, 3.91it/s]
59%|#####8 | 59/100 [00:15<00:10, 3.91it/s]
60%|###### | 60/100 [00:15<00:10, 3.91it/s]
61%|######1 | 61/100 [00:15<00:09, 3.90it/s]
62%|######2 | 62/100 [00:15<00:09, 3.91it/s]
63%|######3 | 63/100 [00:16<00:09, 3.92it/s]
64%|######4 | 64/100 [00:16<00:09, 3.92it/s]
65%|######5 | 65/100 [00:16<00:08, 3.92it/s]
66%|######6 | 66/100 [00:16<00:08, 3.93it/s]
67%|######7 | 67/100 [00:17<00:08, 3.93it/s]
68%|######8 | 68/100 [00:17<00:08, 3.94it/s]
69%|######9 | 69/100 [00:17<00:07, 3.94it/s]
70%|####### | 70/100 [00:17<00:07, 3.94it/s]
71%|#######1 | 71/100 [00:18<00:07, 3.94it/s]
72%|#######2 | 72/100 [00:18<00:07, 3.94it/s]
73%|#######3 | 73/100 [00:18<00:06, 3.94it/s]
74%|#######4 | 74/100 [00:18<00:06, 3.94it/s]
75%|#######5 | 75/100 [00:19<00:06, 3.94it/s]
76%|#######6 | 76/100 [00:19<00:06, 3.95it/s]
77%|#######7 | 77/100 [00:19<00:05, 3.95it/s]
78%|#######8 | 78/100 [00:19<00:05, 3.94it/s]
79%|#######9 | 79/100 [00:20<00:05, 3.94it/s]
80%|######## | 80/100 [00:20<00:05, 3.94it/s]
81%|########1 | 81/100 [00:20<00:04, 3.94it/s]
82%|########2 | 82/100 [00:20<00:04, 3.94it/s]
83%|########2 | 83/100 [00:21<00:04, 3.94it/s]
84%|########4 | 84/100 [00:21<00:04, 3.94it/s]
85%|########5 | 85/100 [00:21<00:03, 3.94it/s]
86%|########6 | 86/100 [00:21<00:03, 3.94it/s]
87%|########7 | 87/100 [00:22<00:03, 3.93it/s]
88%|########8 | 88/100 [00:22<00:03, 3.93it/s]
89%|########9 | 89/100 [00:22<00:02, 3.93it/s]
90%|######### | 90/100 [00:22<00:02, 3.93it/s]
91%|#########1| 91/100 [00:23<00:02, 3.93it/s]
92%|#########2| 92/100 [00:23<00:02, 3.93it/s]
93%|#########3| 93/100 [00:23<00:01, 3.94it/s]
94%|#########3| 94/100 [00:24<00:01, 3.94it/s]
95%|#########5| 95/100 [00:24<00:01, 3.94it/s]
96%|#########6| 96/100 [00:24<00:01, 3.94it/s]
97%|#########7| 97/100 [00:24<00:00, 3.94it/s]
98%|#########8| 98/100 [00:25<00:00, 3.93it/s]
99%|#########9| 99/100 [00:25<00:00, 3.93it/s]
100%|##########| 100/100 [00:25<00:00, 3.93it/s]
100%|##########| 100/100 [00:25<00:00, 3.92it/s]
OrtGradientForwardBackwardOptimizer(model_onnx='ir_version...', weights_to_train="['I0_coeff...", loss_output_name='loss', max_iter=100, training_optimizer_name='SGDOptimizer', batch_size=10, learning_rate=LearningRateSGDNesterov(eta0=0.0001, alpha=0.0001, power_t=0.25, learning_rate='invscaling', momentum=0.9, nesterov=True), value=3.1622776601683795e-05, device='cpu', warm_start=False, verbose=1, validation_every=10, learning_loss=SquareLearningLoss(), enable_logging=False, weight_name=None, learning_penalty=ElasticLearningPenalty(l1=0, l2=0.0001), exc=True)
Let’s see the weights.
state_tensors = train_session.get_state()
And the loss.
print(train_session.train_losses_)
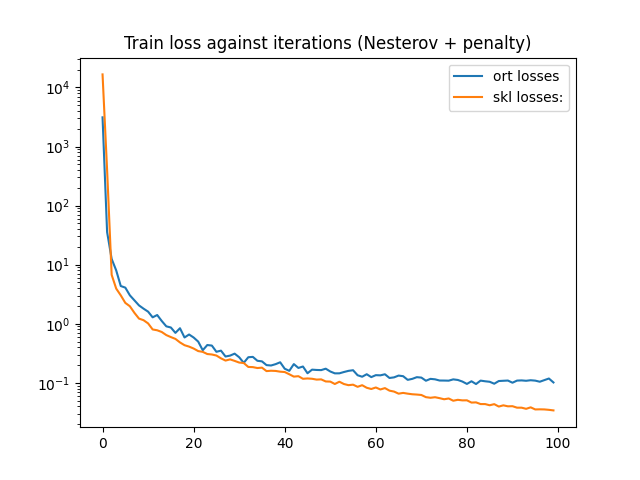
df = DataFrame({'ort losses': train_session.train_losses_,
'skl losses:': nn.loss_curve_})
df.plot(title="Train loss against iterations (Nesterov + penalty)", logy=True)
[3120.9153, 35.6602, 12.506791, 7.9880414, 4.34999, 4.0857024, 3.025379, 2.487744, 2.044642, 1.8003266, 1.6023889, 1.2841896, 1.4042484, 1.1125364, 0.9038065, 0.86354256, 0.7003833, 0.8391579, 0.58535105, 0.6573903, 0.5843982, 0.49862742, 0.35627383, 0.43604764, 0.42697835, 0.3349918, 0.35047787, 0.27878264, 0.28868195, 0.3116556, 0.27076748, 0.21767502, 0.2709586, 0.27462077, 0.23594895, 0.23064284, 0.19930479, 0.19637822, 0.20698488, 0.22259766, 0.17297468, 0.15952353, 0.20729071, 0.17847905, 0.18874472, 0.14511538, 0.16700982, 0.16499269, 0.16403846, 0.17343526, 0.15545487, 0.1445758, 0.14469784, 0.15231642, 0.15936717, 0.16336572, 0.1343075, 0.1267147, 0.13969307, 0.12484948, 0.13471809, 0.13372205, 0.13949239, 0.120709054, 0.12362616, 0.13253187, 0.12938537, 0.112204656, 0.116605245, 0.124557935, 0.122490436, 0.108407795, 0.11660374, 0.11453642, 0.10933198, 0.10916536, 0.108681545, 0.114326745, 0.11175078, 0.10504224, 0.09574188, 0.10619677, 0.09527863, 0.108901694, 0.10615118, 0.10409489, 0.096493244, 0.1071939, 0.1082527, 0.1091876, 0.10033287, 0.10898163, 0.10980664, 0.10820542, 0.1105126, 0.108846195, 0.1043131, 0.111063376, 0.11819006, 0.10140149]
<AxesSubplot: title={'center': 'Train loss against iterations (Nesterov + penalty)'}>
All ONNX graphs#
Method Method save_onnx_graph
can export all the ONNX graph used by the model on disk.
def print_graph(d):
for k, v in sorted(d.items()):
if isinstance(v, dict):
print_graph(v)
else:
print("\n++++++", v.replace("\\", "/"), "\n")
with open(v, "rb") as f:
print(onnx_simple_text_plot(onnx.load(f)))
all_files = train_session.save_onnx_graph('.')
print_graph(all_files)
# import matplotlib.pyplot as plt
# plt.show()
++++++ ./SquareLLoss.learning_loss.loss_grad_onnx_.onnx
opset: domain='' version=14
input: name='X1' type=dtype('float32') shape=[None, None]
input: name='X2' type=dtype('float32') shape=[None, None]
init: name='Mu_Mulcst' type=dtype('float32') shape=(1,) -- array([0.5], dtype=float32)
init: name='Re_Reshapecst' type=dtype('int64') shape=(1,) -- array([-1])
init: name='Mu_Mulcst1' type=dtype('float32') shape=(1,) -- array([-1.], dtype=float32)
Sub(X1, X2) -> Su_C0
Mul(Su_C0, Mu_Mulcst1) -> Y_grad
ReduceSumSquare(Su_C0) -> Re_reduced0
Mul(Re_reduced0, Mu_Mulcst) -> Mu_C0
Reshape(Mu_C0, Re_Reshapecst) -> Y
output: name='Y' type=dtype('float32') shape=None
output: name='Y_grad' type=dtype('float32') shape=None
++++++ ./SquareLLoss.learning_loss.loss_score_onnx_.onnx
opset: domain='' version=14
input: name='X1' type=dtype('float32') shape=[None, None]
input: name='X2' type=dtype('float32') shape=[None, None]
Sub(X1, X2) -> Su_C0
Mul(Su_C0, Su_C0) -> Y
output: name='Y' type=dtype('float32') shape=[None, 1]
++++++ ./ElasticLPenalty.learning_penalty.penalty_grad_onnx_.onnx
opset: domain='' version=14
input: name='X' type=dtype('float32') shape=None
init: name='Mu_Mulcst' type=dtype('float32') shape=(1,) -- array([0.9998], dtype=float32)
init: name='Mu_Mulcst1' type=dtype('float32') shape=(1,) -- array([0.], dtype=float32)
Mul(X, Mu_Mulcst) -> Mu_C0
Sign(X) -> Si_output0
Mul(Si_output0, Mu_Mulcst1) -> Mu_C02
Sub(Mu_C0, Mu_C02) -> Y
output: name='Y' type=dtype('float32') shape=None
++++++ ./ElasticLPenalty.learning_penalty.penalty_onnx_.onnx
opset: domain='' version=14
input: name='loss' type=dtype('float32') shape=None
input: name='W0' type=dtype('float32') shape=None
input: name='W1' type=dtype('float32') shape=None
input: name='W2' type=dtype('float32') shape=None
input: name='W3' type=dtype('float32') shape=None
input: name='W4' type=dtype('float32') shape=None
input: name='W5' type=dtype('float32') shape=None
init: name='Mu_Mulcst' type=dtype('float32') shape=(1,) -- array([0.], dtype=float32)
init: name='Mu_Mulcst1' type=dtype('float32') shape=(1,) -- array([1.e-04], dtype=float32)
init: name='Re_Reshapecst' type=dtype('int64') shape=(1,) -- array([-1])
Abs(W0) -> Ab_Y0
ReduceSum(Ab_Y0) -> Re_reduced0
Mul(Re_reduced0, Mu_Mulcst) -> Mu_C0
Identity(Mu_Mulcst1) -> Mu_Mulcst3
ReduceSumSquare(W0) -> Re_reduced02
Mul(Re_reduced02, Mu_Mulcst1) -> Mu_C02
Add(Mu_C0, Mu_C02) -> Ad_C06
Identity(Mu_Mulcst) -> Mu_Mulcst2
ReduceSumSquare(W1) -> Re_reduced04
Mul(Re_reduced04, Mu_Mulcst3) -> Mu_C04
Abs(W1) -> Ab_Y02
ReduceSum(Ab_Y02) -> Re_reduced03
Mul(Re_reduced03, Mu_Mulcst2) -> Mu_C03
Add(Mu_C03, Mu_C04) -> Ad_C07
Add(Ad_C06, Ad_C07) -> Ad_C05
Abs(W2) -> Ab_Y03
ReduceSum(Ab_Y03) -> Re_reduced05
Identity(Mu_Mulcst1) -> Mu_Mulcst11
ReduceSumSquare(W2) -> Re_reduced06
ReduceSumSquare(W5) -> Re_reduced012
Mul(Re_reduced012, Mu_Mulcst11) -> Mu_C012
ReduceSumSquare(W4) -> Re_reduced010
Identity(Mu_Mulcst) -> Mu_Mulcst4
Mul(Re_reduced05, Mu_Mulcst4) -> Mu_C05
ReduceSumSquare(W3) -> Re_reduced08
Identity(Mu_Mulcst1) -> Mu_Mulcst5
Mul(Re_reduced06, Mu_Mulcst5) -> Mu_C06
Add(Mu_C05, Mu_C06) -> Ad_C08
Add(Ad_C05, Ad_C08) -> Ad_C04
Abs(W3) -> Ab_Y04
ReduceSum(Ab_Y04) -> Re_reduced07
Identity(Mu_Mulcst) -> Mu_Mulcst6
Mul(Re_reduced07, Mu_Mulcst6) -> Mu_C07
Identity(Mu_Mulcst1) -> Mu_Mulcst7
Mul(Re_reduced08, Mu_Mulcst7) -> Mu_C08
Add(Mu_C07, Mu_C08) -> Ad_C09
Add(Ad_C04, Ad_C09) -> Ad_C03
Abs(W4) -> Ab_Y05
ReduceSum(Ab_Y05) -> Re_reduced09
Identity(Mu_Mulcst) -> Mu_Mulcst8
Mul(Re_reduced09, Mu_Mulcst8) -> Mu_C09
Identity(Mu_Mulcst1) -> Mu_Mulcst9
Mul(Re_reduced010, Mu_Mulcst9) -> Mu_C010
Add(Mu_C09, Mu_C010) -> Ad_C010
Add(Ad_C03, Ad_C010) -> Ad_C02
Abs(W5) -> Ab_Y06
ReduceSum(Ab_Y06) -> Re_reduced011
Identity(Mu_Mulcst) -> Mu_Mulcst10
Mul(Re_reduced011, Mu_Mulcst10) -> Mu_C011
Add(Mu_C011, Mu_C012) -> Ad_C011
Add(Ad_C02, Ad_C011) -> Ad_C01
Add(loss, Ad_C01) -> Ad_C0
Reshape(Ad_C0, Re_Reshapecst) -> Y
output: name='Y' type=dtype('float32') shape=[None]
++++++ ./LRateSGDNesterov.learning_rate.axpyw_onnx_.onnx
opset: domain='' version=14
input: name='X1' type=dtype('float32') shape=None
input: name='X2' type=dtype('float32') shape=None
input: name='G' type=dtype('float32') shape=None
input: name='alpha' type=dtype('float32') shape=[1]
input: name='beta' type=dtype('float32') shape=[1]
Mul(X1, alpha) -> Mu_C0
Mul(G, beta) -> Mu_C03
Add(Mu_C0, Mu_C03) -> Z
Mul(Z, beta) -> Mu_C02
Add(Mu_C0, Mu_C02) -> Ad_C0
Add(Ad_C0, X2) -> Y
output: name='Y' type=dtype('float32') shape=None
output: name='Z' type=dtype('float32') shape=None
++++++ ./GradFBOptimizer.model_onnx.onnx
opset: domain='' version=14
input: name='X' type=dtype('float32') shape=[None, 10]
init: name='I0_coefficient' type=dtype('float32') shape=(10, 10)
init: name='I1_intercepts' type=dtype('float32') shape=(1, 10)
init: name='I2_coefficient1' type=dtype('float32') shape=(10, 10)
init: name='I3_intercepts1' type=dtype('float32') shape=(1, 10)
init: name='I4_coefficient2' type=dtype('float32') shape=(10, 1)
init: name='I5_intercepts2' type=dtype('float32') shape=(1, 1) -- array([27.245316], dtype=float32)
init: name='I6_shape_tensor' type=dtype('int64') shape=(2,) -- array([-1, 1])
Cast(X, to=1) -> r0
MatMul(r0, I0_coefficient) -> r1
Add(r1, I1_intercepts) -> r2
Relu(r2) -> r3
MatMul(r3, I2_coefficient1) -> r4
Add(r4, I3_intercepts1) -> r5
Relu(r5) -> r6
MatMul(r6, I4_coefficient2) -> r7
Add(r7, I5_intercepts2) -> r8
Reshape(r8, I6_shape_tensor) -> variable
output: name='variable' type=dtype('float32') shape=[None, 1]
++++++ ./OrtGradientForwardBackwardFunction_140391942413424.train_function_._optimized_pre_grad_model.onnx
opset: domain='' version=14
opset: domain='com.microsoft.experimental' version=1
opset: domain='ai.onnx.preview.training' version=1
opset: domain='ai.onnx.training' version=1
opset: domain='com.ms.internal.nhwc' version=17
opset: domain='org.pytorch.aten' version=1
opset: domain='com.microsoft.nchwc' version=1
opset: domain='ai.onnx.ml' version=3
opset: domain='com.microsoft' version=1
input: name='X' type=dtype('float32') shape=[None, 10]
input: name='I0_coefficient' type=dtype('float32') shape=[10, 10]
input: name='I1_intercepts' type=dtype('float32') shape=[1, 10]
input: name='I2_coefficient1' type=dtype('float32') shape=[10, 10]
input: name='I3_intercepts1' type=dtype('float32') shape=[1, 10]
input: name='I4_coefficient2' type=dtype('float32') shape=[10, 1]
input: name='I5_intercepts2' type=dtype('float32') shape=[1, 1]
init: name='I6_shape_tensor' type=dtype('int64') shape=(2,) -- array([-1, 1])
MatMul(X, I0_coefficient) -> r1
Add(r1, I1_intercepts) -> r2
Relu(r2) -> r3
MatMul(r3, I2_coefficient1) -> r4
Add(r4, I3_intercepts1) -> r5
Relu(r5) -> r6
MatMul(r6, I4_coefficient2) -> r7
Add(r7, I5_intercepts2) -> r8
Reshape(r8, I6_shape_tensor, allowzero=0) -> variable
output: name='variable' type=dtype('float32') shape=[None, 1]
++++++ ./OrtGradientForwardBackwardFunction_140391942413424.train_function_._trained_onnx.onnx
opset: domain='' version=14
opset: domain='com.microsoft.experimental' version=1
opset: domain='ai.onnx.preview.training' version=1
opset: domain='ai.onnx.training' version=1
opset: domain='com.ms.internal.nhwc' version=17
opset: domain='org.pytorch.aten' version=1
opset: domain='com.microsoft.nchwc' version=1
opset: domain='ai.onnx.ml' version=3
opset: domain='com.microsoft' version=1
input: name='X' type=dtype('float32') shape=[None, 10]
input: name='I0_coefficient' type=dtype('float32') shape=[10, 10]
input: name='I1_intercepts' type=dtype('float32') shape=[1, 10]
input: name='I2_coefficient1' type=dtype('float32') shape=[10, 10]
input: name='I3_intercepts1' type=dtype('float32') shape=[1, 10]
input: name='I4_coefficient2' type=dtype('float32') shape=[10, 1]
input: name='I5_intercepts2' type=dtype('float32') shape=[1, 1]
init: name='I6_shape_tensor' type=dtype('int64') shape=(2,) -- array([-1, 1])
init: name='n1_Grad/A_target_shape' type=dtype('int64') shape=(2,) -- array([-1, 10])
init: name='n1_Grad/dY_target_shape' type=dtype('int64') shape=(2,) -- array([-1, 10])
init: name='n4_Grad/A_target_shape' type=dtype('int64') shape=(2,) -- array([-1, 10])
init: name='n4_Grad/dY_target_shape' type=dtype('int64') shape=(2,) -- array([-1, 10])
init: name='n7_Grad/A_target_shape' type=dtype('int64') shape=(2,) -- array([-1, 10])
init: name='n7_Grad/dY_target_shape' type=dtype('int64') shape=(2,) -- array([-1, 1])
MatMul(X, I0_coefficient) -> r1
Add(r1, I1_intercepts) -> r2
Relu(r2) -> r3
MatMul(r3, I2_coefficient1) -> r4
Add(r4, I3_intercepts1) -> r5
Relu(r5) -> r6
MatMul(r6, I4_coefficient2) -> r7
Add(r7, I5_intercepts2) -> r8
Reshape(r8, I6_shape_tensor, allowzero=0) -> variable
YieldOp[com.microsoft](variable, full_shape_outputs=[0]) -> variable_grad
Shape(r8) -> n9_Grad/x_shape
Reshape(variable_grad, n9_Grad/x_shape, allowzero=0) -> r8_grad
Shape(I5_intercepts2) -> n8_Grad/Shape_I5_intercepts2
Shape(r7) -> n8_Grad/Shape_r7
BroadcastGradientArgs[com.microsoft](n8_Grad/Shape_r7, n8_Grad/Shape_I5_intercepts2) -> n8_Grad/ReduceAxes_r7, n8_Grad/ReduceAxes_I5_intercepts2
ReduceSum(r8_grad, n8_Grad/ReduceAxes_I5_intercepts2, noop_with_empty_axes=1, keepdims=1) -> n8_Grad/ReduceSum_r8_grad_for_I5_intercepts2
Reshape(n8_Grad/ReduceSum_r8_grad_for_I5_intercepts2, n8_Grad/Shape_I5_intercepts2, allowzero=0) -> I5_intercepts2_grad
ReduceSum(r8_grad, n8_Grad/ReduceAxes_r7, noop_with_empty_axes=1, keepdims=1) -> n8_Grad/ReduceSum_r8_grad_for_r7
Reshape(n8_Grad/ReduceSum_r8_grad_for_r7, n8_Grad/Shape_r7, allowzero=0) -> r7_grad
Reshape(r7_grad, n7_Grad/dY_target_shape, allowzero=0) -> n7_Grad/dY_reshape_2d
Reshape(r6, n7_Grad/A_target_shape, allowzero=0) -> n7_Grad/A_reshape_2d
Gemm(n7_Grad/A_reshape_2d, n7_Grad/dY_reshape_2d, beta=1.00, transB=0, transA=1, alpha=1.00) -> I4_coefficient2_grad
FusedMatMul[com.microsoft](r7_grad, I4_coefficient2, transBatchB=0, transB=1, alpha=1.00, transA=0, transBatchA=0) -> n7_Grad/PreReduceGrad0
Shape(n7_Grad/PreReduceGrad0) -> n7_Grad/Shape_n7_Grad/PreReduceGrad0
Shape(r6) -> n7_Grad/Shape_r6
BroadcastGradientArgs[com.microsoft](n7_Grad/Shape_r6, n7_Grad/Shape_n7_Grad/PreReduceGrad0) -> n7_Grad/ReduceAxes_r6_for_r6,
ReduceSum(n7_Grad/PreReduceGrad0, n7_Grad/ReduceAxes_r6_for_r6, noop_with_empty_axes=1, keepdims=1) -> n7_Grad/ReduceSum_n7_Grad/PreReduceGrad0_for_r6
Reshape(n7_Grad/ReduceSum_n7_Grad/PreReduceGrad0_for_r6, n7_Grad/Shape_r6, allowzero=0) -> r6_grad
ReluGrad[com.microsoft](r6_grad, r6) -> r5_grad
Shape(I3_intercepts1) -> n5_Grad/Shape_I3_intercepts1
Shape(r4) -> n5_Grad/Shape_r4
BroadcastGradientArgs[com.microsoft](n5_Grad/Shape_r4, n5_Grad/Shape_I3_intercepts1) -> n5_Grad/ReduceAxes_r4, n5_Grad/ReduceAxes_I3_intercepts1
ReduceSum(r5_grad, n5_Grad/ReduceAxes_I3_intercepts1, noop_with_empty_axes=1, keepdims=1) -> n5_Grad/ReduceSum_r5_grad_for_I3_intercepts1
Reshape(n5_Grad/ReduceSum_r5_grad_for_I3_intercepts1, n5_Grad/Shape_I3_intercepts1, allowzero=0) -> I3_intercepts1_grad
ReduceSum(r5_grad, n5_Grad/ReduceAxes_r4, noop_with_empty_axes=1, keepdims=1) -> n5_Grad/ReduceSum_r5_grad_for_r4
Reshape(n5_Grad/ReduceSum_r5_grad_for_r4, n5_Grad/Shape_r4, allowzero=0) -> r4_grad
Reshape(r4_grad, n4_Grad/dY_target_shape, allowzero=0) -> n4_Grad/dY_reshape_2d
Reshape(r3, n4_Grad/A_target_shape, allowzero=0) -> n4_Grad/A_reshape_2d
Gemm(n4_Grad/A_reshape_2d, n4_Grad/dY_reshape_2d, beta=1.00, transB=0, transA=1, alpha=1.00) -> I2_coefficient1_grad
FusedMatMul[com.microsoft](r4_grad, I2_coefficient1, transBatchB=0, transB=1, alpha=1.00, transA=0, transBatchA=0) -> n4_Grad/PreReduceGrad0
Shape(n4_Grad/PreReduceGrad0) -> n4_Grad/Shape_n4_Grad/PreReduceGrad0
Shape(r3) -> n4_Grad/Shape_r3
BroadcastGradientArgs[com.microsoft](n4_Grad/Shape_r3, n4_Grad/Shape_n4_Grad/PreReduceGrad0) -> n4_Grad/ReduceAxes_r3_for_r3,
ReduceSum(n4_Grad/PreReduceGrad0, n4_Grad/ReduceAxes_r3_for_r3, noop_with_empty_axes=1, keepdims=1) -> n4_Grad/ReduceSum_n4_Grad/PreReduceGrad0_for_r3
Reshape(n4_Grad/ReduceSum_n4_Grad/PreReduceGrad0_for_r3, n4_Grad/Shape_r3, allowzero=0) -> r3_grad
ReluGrad[com.microsoft](r3_grad, r3) -> r2_grad
Shape(I1_intercepts) -> n2_Grad/Shape_I1_intercepts
Shape(r1) -> n2_Grad/Shape_r1
BroadcastGradientArgs[com.microsoft](n2_Grad/Shape_r1, n2_Grad/Shape_I1_intercepts) -> n2_Grad/ReduceAxes_r1, n2_Grad/ReduceAxes_I1_intercepts
ReduceSum(r2_grad, n2_Grad/ReduceAxes_I1_intercepts, noop_with_empty_axes=1, keepdims=1) -> n2_Grad/ReduceSum_r2_grad_for_I1_intercepts
Reshape(n2_Grad/ReduceSum_r2_grad_for_I1_intercepts, n2_Grad/Shape_I1_intercepts, allowzero=0) -> I1_intercepts_grad
ReduceSum(r2_grad, n2_Grad/ReduceAxes_r1, noop_with_empty_axes=1, keepdims=1) -> n2_Grad/ReduceSum_r2_grad_for_r1
Reshape(n2_Grad/ReduceSum_r2_grad_for_r1, n2_Grad/Shape_r1, allowzero=0) -> r1_grad
Reshape(r1_grad, n1_Grad/dY_target_shape, allowzero=0) -> n1_Grad/dY_reshape_2d
Reshape(X, n1_Grad/A_target_shape, allowzero=0) -> n1_Grad/A_reshape_2d
Gemm(n1_Grad/A_reshape_2d, n1_Grad/dY_reshape_2d, beta=1.00, transB=0, transA=1, alpha=1.00) -> I0_coefficient_grad
FusedMatMul[com.microsoft](r1_grad, I0_coefficient, transBatchB=0, transB=1, alpha=1.00, transA=0, transBatchA=0) -> n1_Grad/PreReduceGrad0
Shape(n1_Grad/PreReduceGrad0) -> n1_Grad/Shape_n1_Grad/PreReduceGrad0
Shape(X) -> n1_Grad/Shape_X
BroadcastGradientArgs[com.microsoft](n1_Grad/Shape_X, n1_Grad/Shape_n1_Grad/PreReduceGrad0) -> n1_Grad/ReduceAxes_X_for_X,
ReduceSum(n1_Grad/PreReduceGrad0, n1_Grad/ReduceAxes_X_for_X, noop_with_empty_axes=1, keepdims=1) -> n1_Grad/ReduceSum_n1_Grad/PreReduceGrad0_for_X
Reshape(n1_Grad/ReduceSum_n1_Grad/PreReduceGrad0_for_X, n1_Grad/Shape_X, allowzero=0) -> X_grad
output: name='X_grad' type=dtype('float32') shape=[None, 10]
output: name='I0_coefficient_grad' type=dtype('float32') shape=[10, 10]
output: name='I1_intercepts_grad' type=dtype('float32') shape=[1, 10]
output: name='I2_coefficient1_grad' type=dtype('float32') shape=[10, 10]
output: name='I3_intercepts1_grad' type=dtype('float32') shape=[1, 10]
output: name='I4_coefficient2_grad' type=dtype('float32') shape=[10, 1]
output: name='I5_intercepts2_grad' type=dtype('float32') shape=[1, 1]
++++++ ./GradFBOptimizer.zero_onnx_.onnx
opset: domain='' version=14
input: name='X' type=dtype('float32') shape=None
init: name='Mu_Mulcst' type=dtype('float32') shape=(1,) -- array([0.], dtype=float32)
Mul(X, Mu_Mulcst) -> Y
output: name='Y' type=dtype('float32') shape=None
Total running time of the script: ( 1 minutes 8.111 seconds)