Note
Click here to download the full example code
Train a linear regression with forward backward#
This example rewrites Train a linear regression with onnxruntime-training with another
optimizer OrtGradientForwardBackwardOptimizer.
This optimizer relies on class TrainingAgent from
onnxruntime-training. In this case, the user does not have to
modify the graph to compute the error. The optimizer
builds another graph which returns the gradient of every weights
assuming the gradient on the output is known. Finally, the optimizer
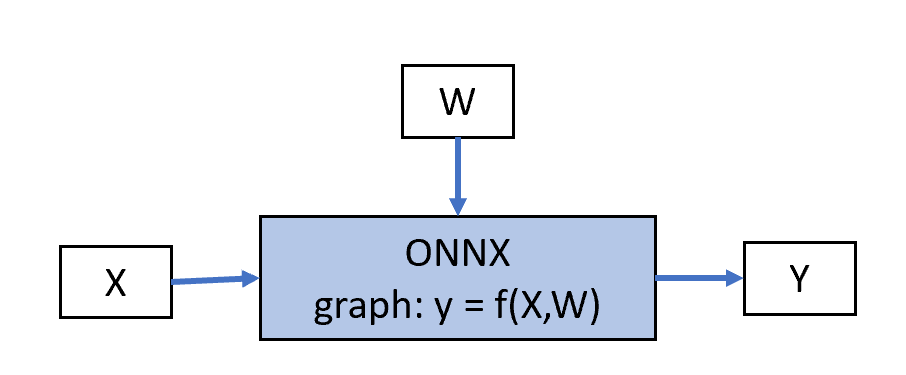
adds the gradients to the weights. To summarize, it starts from the following
graph:
Class OrtGradientForwardBackwardOptimizer
builds other ONNX graph to implement a gradient descent algorithm:
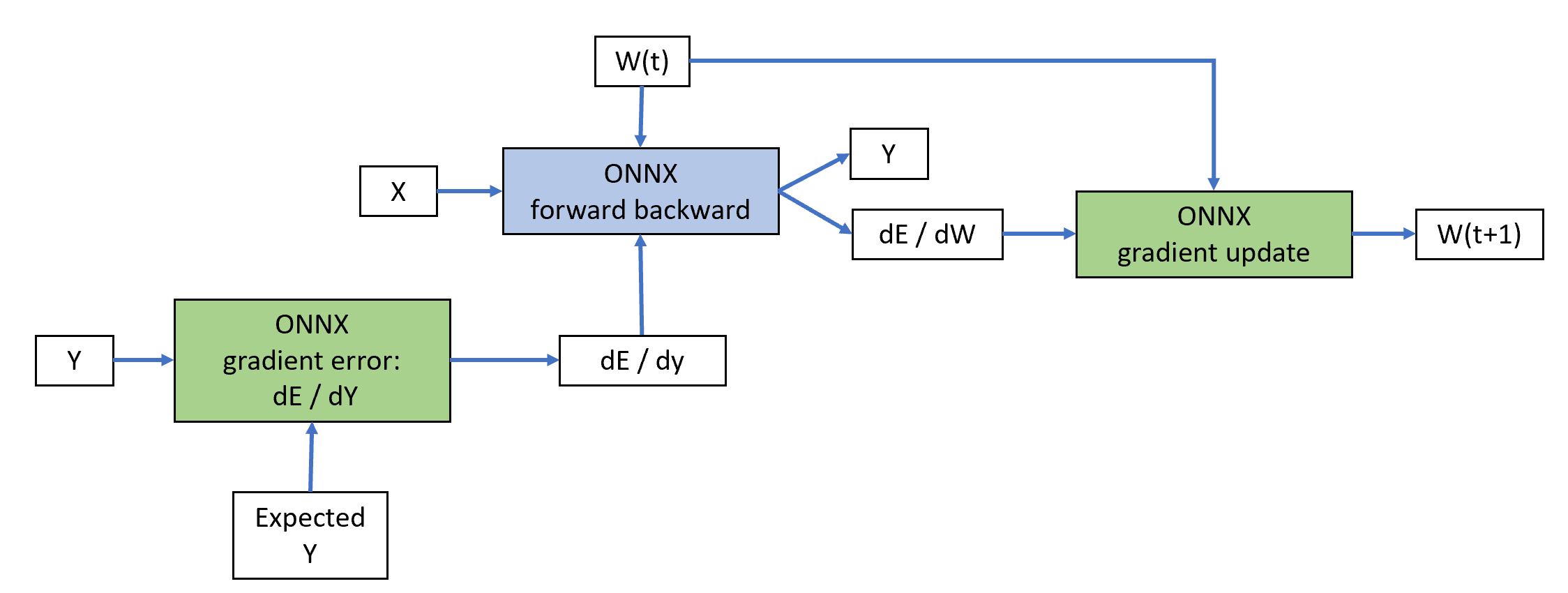
The blue node is built by class TrainingAgent
(from onnxruntime-training). The green nodes are added by
class OrtGradientForwardBackwardOptimizer.
This implementation relies on ONNX to do the computation but it could
be replaced by any other framework such as pytorch. This
design gives more freedom to the user to implement his own training
algorithm.
A simple linear regression with scikit-learn#
from pprint import pprint
import numpy
from pandas import DataFrame
from onnxruntime import get_device
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
from mlprodict.onnx_conv import to_onnx
from onnxcustom.plotting.plotting_onnx import plot_onnxs
from onnxcustom.utils.orttraining_helper import get_train_initializer
from onnxcustom.training.optimizers_partial import (
OrtGradientForwardBackwardOptimizer)
X, y = make_regression(n_features=2, bias=2)
X = X.astype(numpy.float32)
y = y.astype(numpy.float32)
X_train, X_test, y_train, y_test = train_test_split(X, y)
We use a sklearn.neural_network.MLPRegressor.
lr = MLPRegressor(hidden_layer_sizes=tuple(),
activation='identity', max_iter=50,
batch_size=10, solver='sgd',
alpha=0, learning_rate_init=1e-2,
n_iter_no_change=200,
momentum=0, nesterovs_momentum=False)
lr.fit(X, y)
print(lr.predict(X[:5]))
somewhere/workspace/onnxcustom/onnxcustom_UT_39_std/_venv/lib/python3.9/site-packages/sklearn/neural_network/_multilayer_perceptron.py:679: ConvergenceWarning: Stochastic Optimizer: Maximum iterations (50) reached and the optimization hasn't converged yet.
warnings.warn(
[-31.613749 74.62066 1.8960948 34.660263 49.48107 ]
The trained coefficients are:
print("trained coefficients:", lr.coefs_, lr.intercepts_)
trained coefficients: [array([[53.34389 ],
[24.865873]], dtype=float32)] [array([1.7797871], dtype=float32)]
ONNX graph#
Training with onnxruntime-training starts with an ONNX graph which defines the model to learn. It is obtained by simply converting the previous linear regression into ONNX.
onx = to_onnx(lr, X_train[:1].astype(numpy.float32), target_opset=15,
black_op={'LinearRegressor'})
plot_onnxs(onx, title="Linear Regression in ONNX")
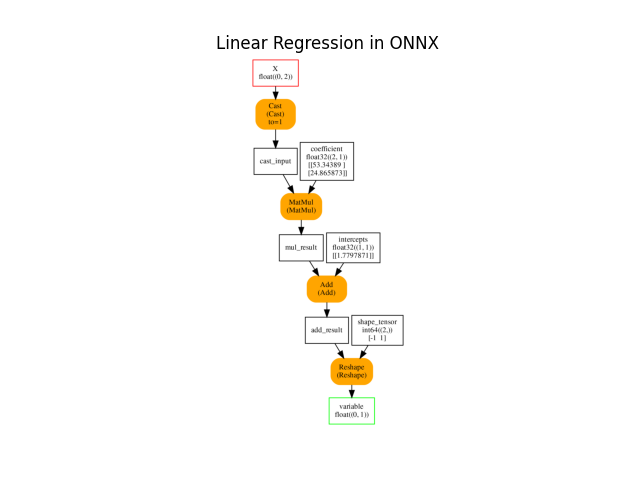
<AxesSubplot: title={'center': 'Linear Regression in ONNX'}>
Weights#
Every initializer is a set of weights which can be trained
and a gradient will be computed for it.
However an initializer used to modify a shape or to
extract a subpart of a tensor does not need training.
get_train_initializer
removes them.
inits = get_train_initializer(onx)
weights = {k: v for k, v in inits.items() if k != "shape_tensor"}
pprint(list((k, v[0].shape) for k, v in weights.items()))
[('coefficient', (2, 1)), ('intercepts', (1, 1))]
Train on CPU or GPU if available#
device = "cuda" if get_device().upper() == 'GPU' else 'cpu'
print(f"device={device!r} get_device()={get_device()!r}")
device='cpu' get_device()='CPU'
Stochastic Gradient Descent#
The training logic is hidden in class
OrtGradientForwardBackwardOptimizer
It follows scikit-learn API (see SGDRegressor.
train_session = OrtGradientForwardBackwardOptimizer(
onx, list(weights), device=device, verbose=1, learning_rate=1e-2,
warm_start=False, max_iter=200, batch_size=10)
train_session.fit(X, y)
0%| | 0/200 [00:00<?, ?it/s]
4%|3 | 7/200 [00:00<00:02, 65.48it/s]
9%|9 | 18/200 [00:00<00:02, 86.17it/s]
14%|#4 | 29/200 [00:00<00:01, 92.97it/s]
20%|## | 40/200 [00:00<00:01, 96.08it/s]
26%|##5 | 51/200 [00:00<00:01, 97.65it/s]
31%|###1 | 62/200 [00:00<00:01, 98.94it/s]
36%|###6 | 73/200 [00:00<00:01, 99.44it/s]
42%|####2 | 84/200 [00:00<00:01, 100.05it/s]
48%|####7 | 95/200 [00:00<00:01, 100.24it/s]
53%|#####3 | 106/200 [00:01<00:00, 100.47it/s]
58%|#####8 | 117/200 [00:01<00:00, 100.65it/s]
64%|######4 | 128/200 [00:01<00:00, 100.41it/s]
70%|######9 | 139/200 [00:01<00:00, 100.58it/s]
75%|#######5 | 150/200 [00:01<00:00, 100.50it/s]
80%|######## | 161/200 [00:01<00:00, 100.57it/s]
86%|########6 | 172/200 [00:01<00:00, 100.71it/s]
92%|#########1| 183/200 [00:01<00:00, 100.66it/s]
97%|#########7| 194/200 [00:01<00:00, 100.83it/s]
100%|##########| 200/200 [00:02<00:00, 98.85it/s]
OrtGradientForwardBackwardOptimizer(model_onnx='ir_version...', weights_to_train=['coefficient', 'intercepts'], loss_output_name='loss', max_iter=200, training_optimizer_name='SGDOptimizer', batch_size=10, learning_rate=LearningRateSGD(eta0=0.01, alpha=0.0001, power_t=0.25, learning_rate='invscaling'), value=0.0026591479484724943, device='cpu', warm_start=False, verbose=1, validation_every=20, learning_loss=SquareLearningLoss(), enable_logging=False, weight_name=None, learning_penalty=NoLearningPenalty(), exc=True)
And the trained coefficients are…
state_tensors = train_session.get_state()
pprint(["trained coefficients:", state_tensors])
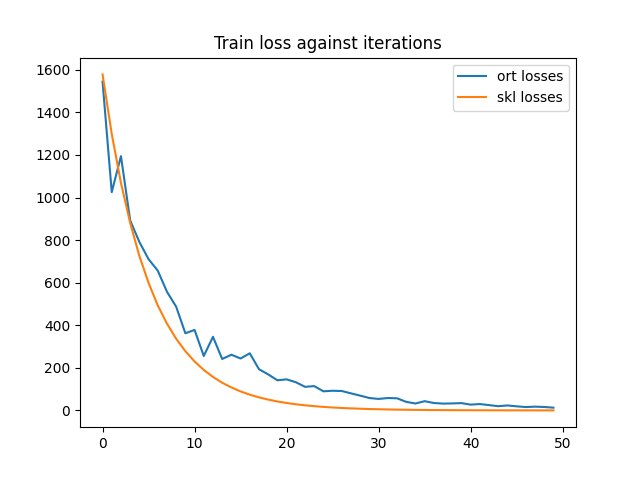
print("last_losses:", train_session.train_losses_[-5:])
min_length = min(len(train_session.train_losses_), len(lr.loss_curve_))
df = DataFrame({'ort losses': train_session.train_losses_[:min_length],
'skl losses': lr.loss_curve_[:min_length]})
df.plot(title="Train loss against iterations")
['trained coefficients:',
[<onnxruntime.capi.onnxruntime_pybind11_state.OrtValue object at 0x7fafc5a82770>,
<onnxruntime.capi.onnxruntime_pybind11_state.OrtValue object at 0x7fafc5b81eb0>]]
last_losses: [0.0054119555, 0.0043852413, 0.00564376, 0.0044368017, 0.0050066994]
<AxesSubplot: title={'center': 'Train loss against iterations'}>
The convergence speed is almost the same.
Gradient Graph#
As mentioned in this introduction, the computation relies on a few more graphs than the initial graph. When the loss is needed but not the gradient, class TrainingAgent creates another graph, faster, with the trained initializers as additional inputs.
onx_loss = train_session.train_session_.cls_type_._optimized_pre_grad_model
plot_onnxs(onx, onx_loss, title=['regression', 'loss'])
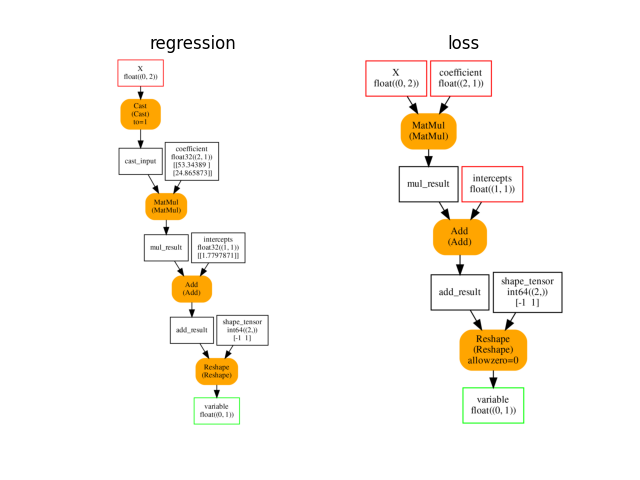
array([<AxesSubplot: title={'center': 'regression'}>,
<AxesSubplot: title={'center': 'loss'}>], dtype=object)
And the gradient.
onx_gradient = train_session.train_session_.cls_type_._trained_onnx
plot_onnxs(onx_loss, onx_gradient, title=['loss', 'gradient + loss'])
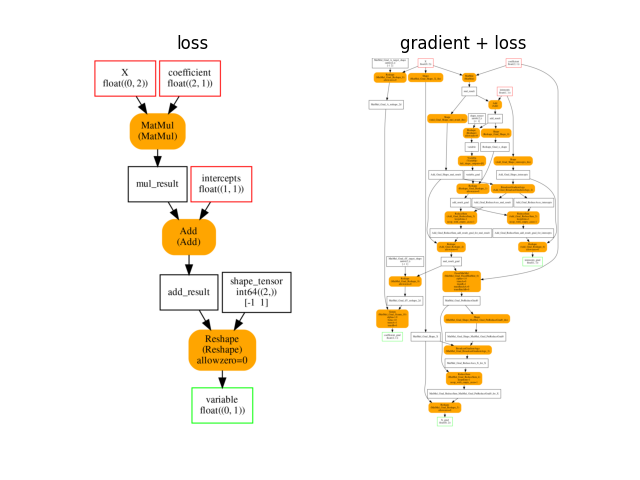
array([<AxesSubplot: title={'center': 'loss'}>,
<AxesSubplot: title={'center': 'gradient + loss'}>], dtype=object)
The last ONNX graphs are used to compute the gradient dE/dY and to update the weights. The first graph takes the labels and the expected labels and returns the square loss and its gradient. The second graph takes the weights and the learning rate as inputs and returns the updated weights. This graph works on tensors of any shape but with the same element type.
plot_onnxs(train_session.learning_loss.loss_grad_onnx_,
train_session.learning_rate.axpy_onnx_,
title=['error gradient + loss', 'gradient update'])
# import matplotlib.pyplot as plt
# plt.show()
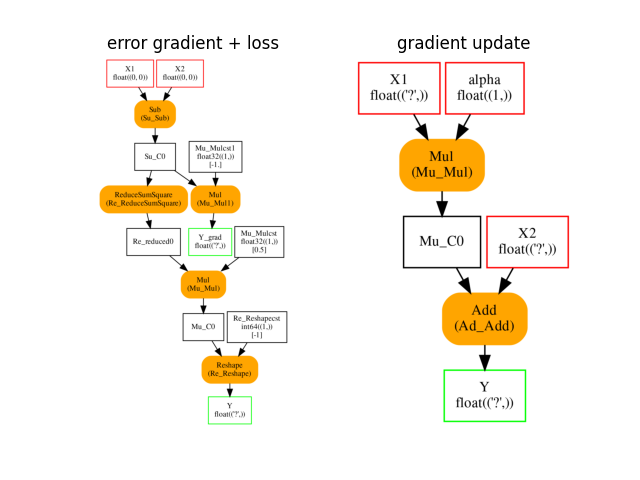
array([<AxesSubplot: title={'center': 'error gradient + loss'}>,
<AxesSubplot: title={'center': 'gradient update'}>], dtype=object)
Total running time of the script: ( 0 minutes 8.743 seconds)